-
PikanavigaatioAjankohtaista io-tech.fi uutiset Uutisia lyhyesti Muu uutiskeskustelu io-tech.fi artikkelit io-techin Youtube-videot Palaute, tiedotukset ja arvonnat
Tietotekniikka Prosessorit, ylikellotus, emolevyt ja muistit Näytönohjaimet Tallennus Kotelot ja virtalähteet Jäähdytys Konepaketit Kannettavat tietokoneet Buildit, setupit, kotelomodifikaatiot & DIY Oheislaitteet ja muut PC-komponentit
Tekniikkakeskustelut Ongelmat Yleinen rautakeskustelu Älypuhelimet, tabletit, älykellot ja muu mobiili Viihde-elektroniikka, audio ja kamerat Elektroniikka, rakentelu ja muut DIY-projektit Internet, tietoliikenne ja tietoturva Käyttäjien omat tuotetestit
Softakeskustelut Pelit, PC-pelaaminen ja pelikonsolit Ohjelmointi, pelikehitys ja muu sovelluskehitys Yleinen ohjelmistokeskustelu Testiohjelmat ja -tulokset
Muut keskustelut Autot ja liikenne Urheilu TV- & nettisarjat, elokuvat ja musiikki Ruoka & juoma Koti ja asuminen Yleistä keskustelua Politiikka ja yhteiskunta Hyvät tarjoukset Tekniikkatarjoukset Pelitarjoukset Ruoka- ja taloustarviketarjoukset Muut tarjoukset
Kauppa-alue
Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Huomio: This feature may not be available in some browsers.
Lisää vaihtoehtoja
Tyylin valinta
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Matikkatriidi - apuja matemaattisiin pulmiin
- Keskustelun aloittaja Tupsa
- Aloitettu
Olen kyllä @Dalle :n kanssa samoilla linjoilla. Satunnaismuuttujahan (esim. X) on kuvaus otosavaruudesta ( = kaikkien alkeistapauksien muodostama joukko) reaaliavaruuteen X: S -> R. Täten otosavaruudessa (S) on oltava tässä tilanteessa 36 alkiota.
Nyt kun hieman palautin mieleeni todennäköisyyslaskentaa, niin nähdäkseni molemmat ovat oikein. Voidaan ajatella että alkeistapaukset ovat noppien heitot, jolloin otosavaruus on kaikki parit (i,j), ja erotus on satunnaismuuttuja. Toisaalta voidaan yhtä hyvin ajatella että kokeen alkeistapaukset (eli se mitä havainnoidaan) ovat noppien silmälukujen erotus.
Kokeillaanpa tänne. f(x)=(5x+x²)/x²+2x-15) funktio pitäisi tehdä taulukko-ohjelmaan siten että voin tehdä taulukon, johon laitan arvoja, joista sitten saisin vastauksen. Eli taulukko johon sijotan eri x arvoja ja taulukko laskee ne automaattisesti. En muista yhtään miten tehtiin, mutta jotenkin niitä soluja ohjelmoitiin. Geogebraa käytän. En löydä netistä ohjeita tähän.
Hommapa menee näin:
1) Kirjoita A-sarakkeeseen halumiasi x:n arvoja (esim. A1 = 1, A2 = 2, ...)
2) Valitse seuraavaksi solu B1 ja paina taulukon vasemmasta yläkulmasta fx-painiketta. Kirjoita B1 soluun mainitsemasi funktio muodossa f(x) = (5*A1+A1^2)/(A1^2+2*A1-15) ja paina enteriä.
3) Lopuksi valitse taas solu B1 ja raahaa solun oikean alakulman sinisestä neliöstä funktio kaikkiin B sarakkeen soluihin
Tämän jälkeen voit halutessasi vaihdella A-sarakkeessa x:n arvoja ja tulokset päivittyvät automaattisesti B-sarakkeeseen.
1) Kirjoita A-sarakkeeseen halumiasi x:n arvoja (esim. A1 = 1, A2 = 2, ...)
2) Valitse seuraavaksi solu B1 ja paina taulukon vasemmasta yläkulmasta fx-painiketta. Kirjoita B1 soluun mainitsemasi funktio muodossa f(x) = (5*A1+A1^2)/(A1^2+2*A1-15) ja paina enteriä.
3) Lopuksi valitse taas solu B1 ja raahaa solun oikean alakulman sinisestä neliöstä funktio kaikkiin B sarakkeen soluihin
Tämän jälkeen voit halutessasi vaihdella A-sarakkeessa x:n arvoja ja tulokset päivittyvät automaattisesti B-sarakkeeseen.
Hommapa menee näin:
1) Kirjoita A-sarakkeeseen halumiasi x:n arvoja (esim. A1 = 1, A2 = 2, ...)
2) Valitse seuraavaksi solu B1 ja paina taulukon vasemmasta yläkulmasta fx-painiketta. Kirjoita B1 soluun mainitsemasi funktio muodossa f(x) = (5*A1+A1^2)/(A1^2+2*A1-15) ja paina enteriä.
3) Lopuksi valitse taas solu B1 ja raahaa solun oikean alakulman sinisestä neliöstä funktio kaikkiin B sarakkeen soluihin
Tämän jälkeen voit halutessasi vaihdella A-sarakkeessa x:n arvoja ja tulokset päivittyvät automaattisesti B-sarakkeeseen.
Siis joo tämän ymmärrän, mutta kun ongelma on etten saa tehtyä funktiosta sellaista automaattista. Tein funktion, mutta mitään ei tapahdu kun vetää arvojen kohdalle sen. Mä en taida ikinä päästä derivointia eteenpäin kun jumitan tässä. Excelissä = merkki tekee funktion ja siihen sitten helppo vetää arvoja, mutta excel taas valittaa joista merkinnöistä kun tulkitsee varmaan potenssin pilkuksi jne. Olisko sulla jotain sivua/youtube kanavaa heittää miten toi tehdään. Menee hermot kun neljänä iltana jo uhrannut illan tähän ongelmaan.
Hei taisinkin onnistua!! avulla tein!
Viimeksi muokattu:
Jos englantia osaat niin voin suositella todella paljon khan academyn videoita, esim https://www.khanacademy.org/math/algebra
Selvitä onko (1,−1,0,2)∈L((1,2,0,1),(2,0,−1,1),(0,1,1,−1)).
Miten ihmeessä tuossa saa mitään aikaiseksi, koska jos alkaa yhtälöryhmää tekemään, niin tulee 3 tuntematonta ja 4 yhtälöä.
c1 + 2c2 = 1
2c1 + c3 = -1
-c2 + c3 = 0
c1 +c2 -c3 = 2
Eli siis miten tuosta mitään matriisia saa aikaan, saati sitten jotain Gaussin Jordanin redusoitua matriisia.
Pitäisi vissiin tulla joku, mutta en tajua, että miten ihmeessä.
c1 = 0
c2 = 0
c3 = 0
0 = 1
Miten ihmeessä tuossa saa mitään aikaiseksi, koska jos alkaa yhtälöryhmää tekemään, niin tulee 3 tuntematonta ja 4 yhtälöä.
c1 + 2c2 = 1
2c1 + c3 = -1
-c2 + c3 = 0
c1 +c2 -c3 = 2
Eli siis miten tuosta mitään matriisia saa aikaan, saati sitten jotain Gaussin Jordanin redusoitua matriisia.
Pitäisi vissiin tulla joku, mutta en tajua, että miten ihmeessä.
c1 = 0
c2 = 0
c3 = 0
0 = 1
Viimeksi muokattu:
Selvitä onko (1,−1,0,2)∈L((1,2,0,1),(2,0,−1,1),(0,1,1,−1)).
Miten ihmeessä tuossa saa mitään aikaiseksi, koska jos alkaa yhtälöryhmää tekemään, niin tulee 3 tuntematonta ja 4 yhtälöä.
c1 + 2c2 = 1
2c1 + c3 = -1
-c2 + c3 = 0
c1 +c2 -c3 = 2
Eli siis miten tuosta mitään matriisia saa aikaan, saati sitten jotain Gaussin Jordanin redusoitua matriisia.
Pitäisi vissiin tulla joku, mutta en tajua, että miten ihmeessä.
c1 = 0
c2 = 0
c3 = 0
0 = 1
No kirjoita yhtälö matriisimuotoon ja käytä Gaussin eliminointia.
Matriisi on [1 2 0 1; 2 0 1 -1;0 -1 1 0;1 1 -1 2].
Tai voit myös laskea tuon determinantin ja todeta determinantti ei ole nolla=> kaikki vektorit lineaarisesti riippumattomia.

Nyt saa selittää sitten todella paksusta rautalangasta.
2) b) Miten jatketaan? Aluksi kai x(5) = 2,40m/s^2 * 5s^2 - 0,12m/s^3 * 5s^3 = 58,2m. Mutta mitä sitten?
Ja kolmostehtävästä ei sitten ole sitäkään vähää käsitystä.
Nopeuden x-komponentti = paikan x-komponentin derivaatta. Eli b) kohdassa lasket x:n derivaatan t:n suhteen ja sijoitat.
Tehtävässä 3 vastaavasti kiihtyvyys on nopeuden derivaatta, eli derivoit nopeuden yhtälöä. Loppu menee samoin kuin 2.
Eli derivaataksi tulee 2tb -3t^2 * c = > (5s)^2 * 2,40m/s^2 - 3(5s)^2 * 0,120m/s^3 = 51 m/sNopeuden x-komponentti = paikan x-komponentin derivaatta. Eli b) kohdassa lasket x:n derivaatan t:n suhteen ja sijoitat.
Tehtävässä 3 vastaavasti kiihtyvyys on nopeuden derivaatta, eli derivoit nopeuden yhtälöä. Loppu menee samoin kuin 2.
Mikä meni taas pieleen?
Eli derivaataksi tulee 2tb -3t^2 * c = > (5s)^2 * 2,40m/s^2 - 3(5s)^2 * 0,120m/s^3 = 51 m/s
Mikä meni taas pieleen?
Derivaatan laskit aivan oikein, mutta sijoitit 5s ihan väärään yhtälöön
2*5*2,4 - 3*5^2*0,12 = 15 m/s
Ehkä kannattaisi jättää yliopistot viisaammille jos virheet on tätä luokkaaDerivaatan laskit aivan oikein, mutta sijoitit 5s ihan väärään yhtälöön
2*5*2,4 - 3*5^2*0,12 = 15 m/s
Viimeksi muokattu:
Onnea fysiikan opiskeluun yliopistossa. Peruskurssit menevät lukiopohjalla vielä helposti tai muuten vaan läpi rämpimällä, mutta myöhempien vuosien kurssit ovat työläitä ja motivaation on oltava kunnossa. Monesti korostetaan sitä "viisautta", mutta motivaatiosta ja istumalihaksista se oikeastaan enemmän on kiinni.Ehkä kannattaisi jättää yliopistot viisaammille jos virheet on tätä luokkaaMutta nyt meni oikein, kiitos!
Ei matikkaa, vaan lukion fysiikka, jota tässä kertailen. Mutten onnistunut googlettamaan sopivampaa ketjua.
Menossa aaltoliike ja siinä mietityttää kirjan pulssin/aaltoliikkeen etenemistä ja heijastumista koskevat ristiriitaisuudet (kts. kuva sinisöidyt kohdat):

Ja sitten toisaalta toisessa esimerkissä havainnollistetaan, kuinka kierrejousen pulssi heijastuu kiinteästi seinään tehdystä jäykästä kytkennästä puolen vaiheen siirrolla ja löysällä kytkennällä samanvaiheisena, mutta sanotaan, että heijastuessaan aalto-opillisesti tiheämmästä aineesta tapahtuu puolikas vaihesiirto ja heijastuessaan aalto-opillisesti harvemmasta aineesta pulssi pysyy samanvaiheisena, ja perään todetaan, että aalto-opillisesti tiheämmäksi sanotaan ainetta, missä aalto kulkee hitaammin ja toisin päin. Mutta eikö tuo jäykkä kytkentä seinään kuvaa aalto-opillisesti harvemman aineen rajapintaa?
Saisko jonkun vääntämään rautalangasta?
Menossa aaltoliike ja siinä mietityttää kirjan pulssin/aaltoliikkeen etenemistä ja heijastumista koskevat ristiriitaisuudet (kts. kuva sinisöidyt kohdat):
Ja sitten toisaalta toisessa esimerkissä havainnollistetaan, kuinka kierrejousen pulssi heijastuu kiinteästi seinään tehdystä jäykästä kytkennästä puolen vaiheen siirrolla ja löysällä kytkennällä samanvaiheisena, mutta sanotaan, että heijastuessaan aalto-opillisesti tiheämmästä aineesta tapahtuu puolikas vaihesiirto ja heijastuessaan aalto-opillisesti harvemmasta aineesta pulssi pysyy samanvaiheisena, ja perään todetaan, että aalto-opillisesti tiheämmäksi sanotaan ainetta, missä aalto kulkee hitaammin ja toisin päin. Mutta eikö tuo jäykkä kytkentä seinään kuvaa aalto-opillisesti harvemman aineen rajapintaa?
Saisko jonkun vääntämään rautalangasta?
Aaltoliikkeitä pohtiessa kannattaa lähteä liikkeelle siitä, että miettii minkälainen aaltoliike on kyseessä, koska se vaikuttaa siihen onko väliaine juuri kyseiselle aaltoliikkeelle tiheää vai harvaa.
- Esimerkki 1: Jos ääniaalto (paineaalto) osuu kiinteän seinän pintaan, niin vaihesiirtoa ei tapahtu, koska ääniaallon aallonnopeus on suurempi kiinteässä aineessa kuin ilmassa (akustinen impedanssi).
- Esimerkki 2: Jos valo (sähkömagneettinen aalto) osuu lasin pintaan, niin vaihesiirto tapahtuu, koska lasin heijastuskerroin on suurempi kuin ilman. Valo siis kulkee lasin sisällä hiljempaa kuin ilmassa eli lasi on ilman suhteen aalto-opillisesti tiheämpää väliainetta.
Samalla tavalla voi lähteä miettimään millainen aalto on kyseessä tuossa jousiesimerkissä? Ja miksi kiinteä seinäkiinnitys aiheuttaa vaihesiirron.
- Esimerkki 1: Jos ääniaalto (paineaalto) osuu kiinteän seinän pintaan, niin vaihesiirtoa ei tapahtu, koska ääniaallon aallonnopeus on suurempi kiinteässä aineessa kuin ilmassa (akustinen impedanssi).
- Esimerkki 2: Jos valo (sähkömagneettinen aalto) osuu lasin pintaan, niin vaihesiirto tapahtuu, koska lasin heijastuskerroin on suurempi kuin ilman. Valo siis kulkee lasin sisällä hiljempaa kuin ilmassa eli lasi on ilman suhteen aalto-opillisesti tiheämpää väliainetta.
Samalla tavalla voi lähteä miettimään millainen aalto on kyseessä tuossa jousiesimerkissä? Ja miksi kiinteä seinäkiinnitys aiheuttaa vaihesiirron.
Aaltoliikkeitä pohtiessa kannattaa lähteä liikkeelle siitä, että miettii minkälainen aaltoliike on kyseessä, koska se vaikuttaa siihen onko väliaine juuri kyseiselle aaltoliikkeelle tiheää vai harvaa.
- Esimerkki 1: Jos ääniaalto (paineaalto) osuu kiinteän seinän pintaan, niin vaihesiirtoa ei tapahtu, koska ääniaallon aallonnopeus on suurempi kiinteässä aineessa kuin ilmassa (akustinen impedanssi).
- Esimerkki 2: Jos valo (sähkömagneettinen aalto) osuu lasin pintaan, niin vaihesiirto tapahtuu, koska lasin heijastuskerroin on suurempi kuin ilman. Valo siis kulkee lasin sisällä hiljempaa kuin ilmassa eli lasi on ilman suhteen aalto-opillisesti tiheämpää väliainetta.
Samalla tavalla voi lähteä miettimään millainen aalto on kyseessä tuossa jousiesimerkissä? Ja miksi kiinteä seinäkiinnitys aiheuttaa vaihesiirron.
Mutta eikös kiinteä kytkentä seinään kierrejouselle (ja lähtökohtaisesti kaikille muillekin mekaanisille aalloille, niin kuin ääniaalloille kuten sanoit) meinaa aalto-opillisesti harvemman aineen rajapintaa?
Mmmh mitenhän minä tämän selittäisin. Kiinnitetyn jousen tapauksessa ajatellaan, että se kiinnityspiste ei pysty liikkumaan ollenkaan, jolloin kierrejousessa etenevän aallon nopeus on 0 tässä kyseisessä pisteessä. Tämähän tarkoittaa sitä, että seinän aalto-opillinen tiheys on ääretön.Mutta eikös kiinteä kytkentä seinään kierrejouselle (ja lähtökohtaisesti kaikille muillekin mekaanisille aalloille, niin kuin ääniaalloille kuten sanoit) meinaa aalto-opillisesti harvemman aineen rajapintaa?
Lisää fysiikkaa: Aaltoliike, pallopeilit:

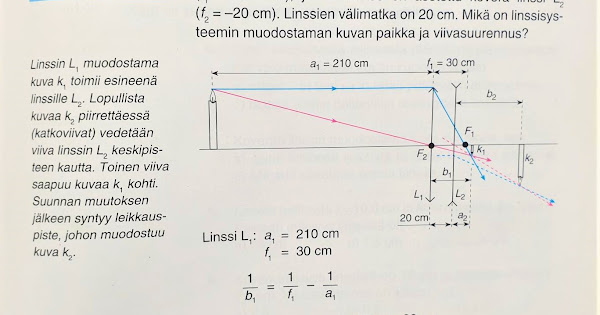
Muodostuuko koveran pallonpeilin polttopiisteellä esineestä kuvaa lainkaan? Ainakin esimerkkikuvien tilanne näyttää, ettei muodostuisi (2. alin vasemman laidan pikkukuva).
Ja onko kaksoiskuperan linssin tapauksessa sama tilanne (pikkukuva d)):

edit: Ja onko viivasuurennus linssisysteemeillä (useammallakin kuin kahdella linssillä) kaikkien linssien suurennusten tulo? m=m1*m2*...
Jos täältä löytyy parempi ketju näillä fyssan (tai kemman) kysymyksille, niin vinkatkaa.
edit2: Lisää: Meneekö esimerkin kuvan k2 varsinainen piirtosääntö niin, että diagonaalisuuntaisen sinisen katkoviivan jatke kulkee polttopisteen F2 kautta, sitä ei vain mainita?
Muodostuuko koveran pallonpeilin polttopiisteellä esineestä kuvaa lainkaan? Ainakin esimerkkikuvien tilanne näyttää, ettei muodostuisi (2. alin vasemman laidan pikkukuva).
Ja onko kaksoiskuperan linssin tapauksessa sama tilanne (pikkukuva d)):
edit: Ja onko viivasuurennus linssisysteemeillä (useammallakin kuin kahdella linssillä) kaikkien linssien suurennusten tulo? m=m1*m2*...
Jos täältä löytyy parempi ketju näillä fyssan (tai kemman) kysymyksille, niin vinkatkaa.
edit2: Lisää: Meneekö esimerkin kuvan k2 varsinainen piirtosääntö niin, että diagonaalisuuntaisen sinisen katkoviivan jatke kulkee polttopisteen F2 kautta, sitä ei vain mainita?
Viimeksi muokattu:
Kuvan perusteella näyttää siltä, että koveran peilin polttopisteessä olevasta esineestä ei muodostu kuvaa. Linssiyhtälöä katsomalla varmaan tulee selitys tuolle (1/a + 1/b = 1/f). Jos polttopiste f ja kuva a ovat samoja, niin 1/b pitää olla yhtälössä 0. Tällöin b menee äärettömään, eli kuvaa ei muodostu minnekään.
Tämä linssiyhtälön tilanne pätenee myös toiseen linkkaamaasi kuvan tilanteeseen (kupera linssi).
Viivasuurennuksissa taisi tosiaan mennä tolleen kertomalla...
Alimpaan kysymykseesi vastaten - oikeanpuolinen linssi taitaa olla kovera. Ensimmäisen linssin tuottama kuva toimii sille esineenä. Ensimmäisen linssin muodostamasta kuvasta menee vaakasuorakatkoviiva tälle koveralle linssi ja linssin hajautunut suunta tulee polttopisteestä kuten arvelit.
Tämä linssiyhtälön tilanne pätenee myös toiseen linkkaamaasi kuvan tilanteeseen (kupera linssi).
Viivasuurennuksissa taisi tosiaan mennä tolleen kertomalla...
Alimpaan kysymykseesi vastaten - oikeanpuolinen linssi taitaa olla kovera. Ensimmäisen linssin tuottama kuva toimii sille esineenä. Ensimmäisen linssin muodostamasta kuvasta menee vaakasuorakatkoviiva tälle koveralle linssi ja linssin hajautunut suunta tulee polttopisteestä kuten arvelit.
Yksinkertainen murtolukutehtävä jota en saa automaattiselle tarkastimelle läpi hyväksytysti:
3/(y-2) - 2/(2-y)
Tästä saan vastaukseksi 5/(y-2), mikä on ohjelman mukaan oikein, mutta ei kelpaa lopulliseksi vastaukseksi. Saako tuon jotenkin vielä sievennettyä, mitä en vaan itse ymmärrä? yritin myös vaihtoehtoisella vastauksella -5/(2-y), mutta sekään ei kelvannut.
edit. näin 3,5h myöhemmin voin todeta että kyllä nää on vaan ihan päin persettä laadittuja tehtäviä
3/(y-2) - 2/(2-y)
Tästä saan vastaukseksi 5/(y-2), mikä on ohjelman mukaan oikein, mutta ei kelpaa lopulliseksi vastaukseksi. Saako tuon jotenkin vielä sievennettyä, mitä en vaan itse ymmärrä? yritin myös vaihtoehtoisella vastauksella -5/(2-y), mutta sekään ei kelvannut.
edit. näin 3,5h myöhemmin voin todeta että kyllä nää on vaan ihan päin persettä laadittuja tehtäviä

Viimeksi muokattu:
Yksinkertainen murtolukutehtävä jota en saa automaattiselle tarkastimelle läpi hyväksytysti:
3/(y-2) - 2/(2-y)
Tästä saan vastaukseksi 5/(y-2), mikä on ohjelman mukaan oikein, mutta ei kelpaa lopulliseksi vastaukseksi. Saako tuon jotenkin vielä sievennettyä, mitä en vaan itse ymmärrä? yritin myös vaihtoehtoisella vastauksella -5/(2-y), mutta sekään ei kelvannut.
edit. näin 3,5h myöhemmin voin todeta että kyllä nää on vaan ihan päin persettä laadittuja tehtäviä
Se ei sitä varmaankaan vastaukseksi hyväksy, koska mielestäni se on väärin. Itse saan tulokseksi (5y - 8)/(y-2)^2.
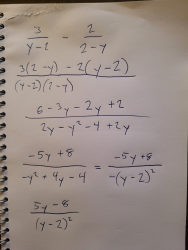
Jos ei käsinlasku suju, niin opetelkaa käyttämään vaikka Wolfram alphaa:
simplify 3/(y-2) - 2/(2-y) - Wolfram|Alpha

simplify 3/(y-2) - 2/(2-y) - Wolfram|Alpha
Se ei sitä varmaankaan vastaukseksi hyväksy, koska mielestäni se on väärin. Itse saan tulokseksi (5y - 8)/(y-2)^2.
Hupsistakeikkaa, ei näköjään luonnistu enää ollenkaan yksinkertaisetkaan yhtälöt. Takaisin koulunpenkille siisJos ei käsinlasku suju, niin opetelkaa käyttämään vaikka Wolfram alphaa:
simplify 3/(y-2) - 2/(2-y) - Wolfram|Alpha

Missäköhän kohdassa se oma ryssiminen tulikaan? Pikaisella tarkistuksella en edes löydä virhettä.
EDIT: Huomasinkin, 2*2 ei ole 2 vaan 4. Ja sitten tulee tosiaan tuo sama Wolframin vastaus itsellekin, eli 5/(y-2)
Viimeksi muokattu:
Joo, siinä oli itsellä useampikin aivopieru. En oivaltanut tuota helpompaa tapaa sieventää koko pakettia. Lähdin sitten nimittäjäksi laventamaan samoja arvoja ja niiden pyörittämisessä kävi tuo 2*2 != 2 moka. Eli putkeenhan se meniMiten sä saat tuon laskettua noin vaikeasti.
Kerrot vaan vaikka jälkimmäisen murtoluvun ylä- ja alapuolen ensin -1:llä (ei muuta arvoa), jolloin

- Liittynyt
- 18.12.2019
- Viestejä
- 156
”Saarella on 12 miestä, joista yksi on eripainoinen kuin muut. Muut miehet painavat kaikki yhtä paljon. Käytössäsi on vaaka. Miten saat selville kolmella punnituksella, kuka miehistä on eripainoinen, ja onko hän painavampi vai kevyempi kuin muut?
Kysytty eri versioina Googlen ja Amazonin työhaastattelussa.”
Tällainen oli tämän päivän Helsingin Sanomissa. Netissä juttu vain tilaajille.

 www.hs.fi
www.hs.fi
Tässä hesarin vastaus ongelmaan:
Selvennyksenä tehtävään sen verran, että kyseessä on tasapainovaaka. Eli ei ole vaaka, joka näyttää painon numeroina. En täysin ymmärrä Hesarin vastausta. Itse saan tuloksen selvitettyä neljällä punnituksella. Pystyykö joku fiksumpi kirjoittamaan auki jokaisen punnituksen. Hesarin vastaus jotenkin skippas toisen punnituksen, jossa selvitetään mikä kolmesta ryhmästä on painavampi tai kevyempi kahta muuta ryhmää.
Kysytty eri versioina Googlen ja Amazonin työhaastattelussa.”
Tällainen oli tämän päivän Helsingin Sanomissa. Netissä juttu vain tilaajille.

Rekrytointi | Testaa, oletko tarpeeksi fiksu Googlelle. Tällaisia aivopähkinöitä huippufirmat kysyvät haastattelussa.
HS Visio selvitti matemaatikon kanssa, kuinka vaikeita knoppeja työnhakijoilta Piilaaksossa kysytään.
Tässä hesarin vastaus ongelmaan:
Ratkaisu:
Miehet pitää jakaa kolmeen ryhmään:
{x1, x2, x3, x4}, {y1, y2, y3, y4}, {z1, z2, z3, z4}.
Punnitaan ensin ryhmä {x1, x2, x3, x4} versus {y1, y2, y3, y4}. Katsotaan siis, ovatko ryhmät samanpainoiset vai onko toinen painavampi. Jatko riippuu ensimmäisen punnituksen tuloksesta. Seuraavaksi ryhmistä vaihdetaan päittäin yksi mies. Ratkaisu etenee tapaus kerrallaan.
Esimerkiksi:
Kun {y1, y2, y3, y4} on painavampi kuin {x1, x2, x3, x4}
ja {z1, z2, z3, x4} on painavampi kuin {x1, x2, x3, y4},
joukossa {x1, x2, x3} täytyy olla muita kevyempi mies.
Jos x1 ja x2 ovat samanpainoisia, x3 on kevyempi kuin muut miehet.
Miehet pitää jakaa kolmeen ryhmään:
{x1, x2, x3, x4}, {y1, y2, y3, y4}, {z1, z2, z3, z4}.
Punnitaan ensin ryhmä {x1, x2, x3, x4} versus {y1, y2, y3, y4}. Katsotaan siis, ovatko ryhmät samanpainoiset vai onko toinen painavampi. Jatko riippuu ensimmäisen punnituksen tuloksesta. Seuraavaksi ryhmistä vaihdetaan päittäin yksi mies. Ratkaisu etenee tapaus kerrallaan.
Esimerkiksi:
Kun {y1, y2, y3, y4} on painavampi kuin {x1, x2, x3, x4}
ja {z1, z2, z3, x4} on painavampi kuin {x1, x2, x3, y4},
joukossa {x1, x2, x3} täytyy olla muita kevyempi mies.
Jos x1 ja x2 ovat samanpainoisia, x3 on kevyempi kuin muut miehet.
Selvennyksenä tehtävään sen verran, että kyseessä on tasapainovaaka. Eli ei ole vaaka, joka näyttää painon numeroina. En täysin ymmärrä Hesarin vastausta. Itse saan tuloksen selvitettyä neljällä punnituksella. Pystyykö joku fiksumpi kirjoittamaan auki jokaisen punnituksen. Hesarin vastaus jotenkin skippas toisen punnituksen, jossa selvitetään mikä kolmesta ryhmästä on painavampi tai kevyempi kahta muuta ryhmää.
”Saarella on 12 miestä, joista yksi on eripainoinen kuin muut. Muut miehet painavat kaikki yhtä paljon. Käytössäsi on vaaka. Miten saat selville kolmella punnituksella, kuka miehistä on eripainoinen, ja onko hän painavampi vai kevyempi kuin muut?
Kysytty eri versioina Googlen ja Amazonin työhaastattelussa.”
Tällainen oli tämän päivän Helsingin Sanomissa. Netissä juttu vain tilaajille.
Selvennyksenä tehtävään sen verran, että kyseessä on tasapainovaaka. Eli ei ole vaaka, joka näyttää painon numeroina. En täysin ymmärrä Hesarin vastausta. Itse saan tuloksen selvitettyä neljällä punnituksella. Pystyykö joku fiksumpi kirjoittamaan auki jokaisen punnituksen. Hesarin vastaus jotenkin skippas toisen punnituksen, jossa selvitetään mikä kolmesta ryhmästä on painavampi tai kevyempi kahta muuta ryhmää.
Versio 2:
1) Punnitaan {x1,x2,x3,x4} vs {y1,y2,y3,y4}. Jos yhtäsuuret, mies on joukossa {z1,z2,z3,z4}.
Oletetaan, että {x1,x2,x3,x4}<{y1,y2,y3,y4}
2) Punnitaan {x1,y1,y2} vs {x2,y3,y4}.
jos =, niin mies on joko x3 tai x4.
jos <, niin mies on joko y3 tai y4 (paivavin), tai x1 (kevein)
3) punnitaan y3 vs y4. Paivavin on kysytty mies.
Viimeksi muokattu:
- Liittynyt
- 07.06.2017
- Viestejä
- 6 114
Ei vaan juurikin kuten kysymys on aseteltu eli eripainoinen. Jos tiedettäisiin etukäteen onko se eripainoinen esim painavampi niin tehtävä olisi paljon helpompi:Edit. Uskoakseni tässä pitää tietää etukäteen haetaanko painavinta vai keveintä.
Ensin ryhmät vaa'alle ja jos eka punnitus olisi tasapeli niin painavin on mittaamattomassa ryhmässä, muuten vaa'an osoittamassa ryhmässä.
Sitten ne neljä jäljelle jäänyttä kahdesti puolitettuna selviäisi se painavin.
- Liittynyt
- 07.06.2017
- Viestejä
- 6 114
Eikös tuo hesarinkin tapa ole silti oikein?Ratkaisu päivitetty. HS:n ratkaisu on väärin, sillä se olettaa että tiedetään haetaanko raskainta vai keveintä etukäteen.
Punnitaan ensin ryhmä {x1, x2, x3, x4} versus {y1, y2, y3, y4}. Katsotaan siis, ovatko ryhmät samanpainoiset vai onko toinen painavampi. Jatko riippuu ensimmäisen punnituksen tuloksesta. Seuraavaksi ryhmistä vaihdetaan päittäin yksi mies. Ratkaisu etenee tapaus kerrallaan.
Esimerkiksi:
Kun {y1, y2, y3, y4} on painavampi kuin {x1, x2, x3, x4}
ja {z1, z2, z3, x4} on painavampi kuin {x1, x2, x3, y4},
joukossa {x1, x2, x3} täytyy olla muita kevyempi mies.
Jos x1 ja x2 ovat samanpainoisia, x3 on kevyempi kuin muut miehet.
Kun vertaavat tuohon varmasti oikean painoiseen z ryhmään kun:
{z1, z2, z3, x4} on painavampi kuin {x1, x2, x3, y4} -> jos tuossa punnituksessa jälkimmäinen olisi painavampi -> silloin joko y4 on painava tai x4 kevyt. Jos ne olisi yhtäpainavat niin yhtälö jatkuisi vain muutoksella että joukossa (y1,y2,y3) on joku painavampi vrt esimerkin (x1,x2,x3) kevyempi.
Viimeksi muokattu:
- Liittynyt
- 18.12.2019
- Viestejä
- 156
@kajakkivajakki Voisitko vielä laittaa punnitukset steppeinä 1, 2 ja 3. En nimittäin vieläkään ymmärrä miten tämä menee. Ei vaan mene itsellä millään jakeluun.
- Liittynyt
- 07.06.2017
- Viestejä
- 6 114
Aloitan nyt ihan alusta siis:
Ekaksi jaetaan 12 joukko kolmeen 4 miehen ryhmään (4x,4y,4z).
Punnitus 1: Laitetaan vaakaan kaksi 4 rypästä -> tästä selviää varmasti vain se joukko, jossa ei ole eripainoista. Jos joukko x ja y on vaaterissa niin joukko z on se jossa on eripainoinen. Jos punnituksessa sattuu käymään niin että se z on eripainoinen niin ongelman ratkaisu on hieman helpompi, mutta koska tuo on epätodennäköisin skenaario niin jatketaan hesarin malliin että eripainoinen on joko x tai y.
Punnituksen tulos siis on: Kun {y1, y2, y3, y4} on painavampi kuin {x1, x2, x3, x4} ->josta voidaan päätellä että joukossa y on keskimääräistä painavampi tai joukossa x on keskimääräistä kevyempi mies, ei toisinpäin eli tämä informaatio auttaa jatkossa.
Punnitus 2: Yksinkertaistetaan hieman eli kun joukko z:n miehet on varmasti oikean painoisia kaikki niin niitä ei tarvi enää eritellä numeroilla. Laitetaan vaakaan toiselle puolelle 3 varmasti oikeanpainoista ja niiden kaveriksi yksi mahdollisesti väärän painoinen x4(kevyt) ja oikealle puolelle x joukon muut miehet sekä lisäksi yksi painavammalta puolelta eli y4
Punnituksen 2 tulos siis on {z, z, z, x4} on painavampi kuin {x1, x2, x3, y4} -> joukossa {x1, x2, x3} täytyy olla muita kevyempi mies. tästä voidaan siis päätellä tuo mitä kirjoitin edellisessä viestissä eli jos tuossa punnituksessa jälkimmäinen olisi painavampi -> silloin joko y4 on painava tai x4 kevyt. Jos ne olisi yhtäpainavat niin yhtälö jatkuisi vain muutoksella että joukossa (y1,y2,y3) (koska ne on ainoat jotka ei ole tässä punnituksessa) on joku painavampi vrt esimerkin (x1,x2,x3) kevyempi. Jos nyt sattuisi ainoaksi vertailupariksi tuo tapaus, että pitää verrata onko x4 kevyt vai y4 raskas niin punnittaisiin jompikumpi varmasti oikeanpainoisen z kanssa ja vaaka kertoisi tuloksen koska jos sattuisi että ovat vaaterissa niin puntarin ulkopuolelle jääneen painoryhmä tiedetään ensimmäisestä punnituksesta.
Punnitus 3: Jos x1 ja x2 ovat samanpainoisia, x3 on kevyempi kuin muut miehet. Sama päätelmä kuin ylläolevasa x4/y4 eli edellisillä punnituksilla on saatu eroteltua joukko kevyisiin tai raskaisiin ja tämä viimeinen punnitus erottelee sen joukon eripainoisen varmasti.
Melkoinen sepustus, toivotaan että logiikka aukeni
Ekaksi jaetaan 12 joukko kolmeen 4 miehen ryhmään (4x,4y,4z).
Punnitus 1: Laitetaan vaakaan kaksi 4 rypästä -> tästä selviää varmasti vain se joukko, jossa ei ole eripainoista. Jos joukko x ja y on vaaterissa niin joukko z on se jossa on eripainoinen. Jos punnituksessa sattuu käymään niin että se z on eripainoinen niin ongelman ratkaisu on hieman helpompi, mutta koska tuo on epätodennäköisin skenaario niin jatketaan hesarin malliin että eripainoinen on joko x tai y.
Punnituksen tulos siis on: Kun {y1, y2, y3, y4} on painavampi kuin {x1, x2, x3, x4} ->josta voidaan päätellä että joukossa y on keskimääräistä painavampi tai joukossa x on keskimääräistä kevyempi mies, ei toisinpäin eli tämä informaatio auttaa jatkossa.
Punnitus 2: Yksinkertaistetaan hieman eli kun joukko z:n miehet on varmasti oikean painoisia kaikki niin niitä ei tarvi enää eritellä numeroilla. Laitetaan vaakaan toiselle puolelle 3 varmasti oikeanpainoista ja niiden kaveriksi yksi mahdollisesti väärän painoinen x4(kevyt) ja oikealle puolelle x joukon muut miehet sekä lisäksi yksi painavammalta puolelta eli y4
Punnituksen 2 tulos siis on {z, z, z, x4} on painavampi kuin {x1, x2, x3, y4} -> joukossa {x1, x2, x3} täytyy olla muita kevyempi mies. tästä voidaan siis päätellä tuo mitä kirjoitin edellisessä viestissä eli jos tuossa punnituksessa jälkimmäinen olisi painavampi -> silloin joko y4 on painava tai x4 kevyt. Jos ne olisi yhtäpainavat niin yhtälö jatkuisi vain muutoksella että joukossa (y1,y2,y3) (koska ne on ainoat jotka ei ole tässä punnituksessa) on joku painavampi vrt esimerkin (x1,x2,x3) kevyempi. Jos nyt sattuisi ainoaksi vertailupariksi tuo tapaus, että pitää verrata onko x4 kevyt vai y4 raskas niin punnittaisiin jompikumpi varmasti oikeanpainoisen z kanssa ja vaaka kertoisi tuloksen koska jos sattuisi että ovat vaaterissa niin puntarin ulkopuolelle jääneen painoryhmä tiedetään ensimmäisestä punnituksesta.
Punnitus 3: Jos x1 ja x2 ovat samanpainoisia, x3 on kevyempi kuin muut miehet. Sama päätelmä kuin ylläolevasa x4/y4 eli edellisillä punnituksilla on saatu eroteltua joukko kevyisiin tai raskaisiin ja tämä viimeinen punnitus erottelee sen joukon eripainoisen varmasti.
Melkoinen sepustus, toivotaan että logiikka aukeni
- Liittynyt
- 18.12.2019
- Viestejä
- 156
Melkoinen sepustus, toivotaan että logiikka aukeni
No nyt tämä aukesi. Suurkiitos!
Simppeli fyssa-asia: Opettajan oppaan mukaan kuvan kirjan tehtävän 8 oikea vastaus on e), missä ei minusta ole mitään järkeä. Toisaalta taulukoiden mukaan heliumin kiehumispiste 1 ATM:ssä on noin -268 C. Eli kirja väärässä?
- Liittynyt
- 07.06.2021
- Viestejä
- 2 353
Ihan oikealtahan tuo vaikuttaa. Absoluuttisessa nollapisteessä molekyylien liike on lähes nolla, täten väite on epätosi.Simppeli fyssa-asia: Opettajan oppaan mukaan kuvan kirjan tehtävän 8 oikea vastaus on e), missä ei minusta ole mitään järkeä. Toisaalta taulukoiden mukaan heliumin kiehumispiste 1 ATM:ssä on noin -268 C. Eli kirja väärässä?
Mikä sinusta on oikea vastaus?
Ihan oikealtahan tuo vaikuttaa. Absoluuttisessa nollapisteessä molekyylien liike on lähes nolla, täten väite on epätosi.
Mikä sinusta on oikea vastaus?
Anteeksi, kirjoitusvirhe: Opettajan oppaan mukaan oikea vastan on c), eli ollaan molemmat samaa mieltä.

Niin ja helium on absoluuttisessa nollassa paineesta riippuen joko supranestettä tai kiinteää, ei tavallista nestettä.
Ja tosiaan vaikka tuossa vaiheessa fysiikan opiskelua olomuotoja olisikin vain kolme, niin sehän tosiaan olisi muuttunut nesteeksi jo huomattavasti lämpimämmässä.
Ja tosiaan vaikka tuossa vaiheessa fysiikan opiskelua olomuotoja olisikin vain kolme, niin sehän tosiaan olisi muuttunut nesteeksi jo huomattavasti lämpimämmässä.
Toivottavasti tämä ei johda herneisiin nenissä, kun käytän ketjua myös kemian ja fyssan kysymyksille.  Pakko saada tämä vuosia kirjassa kummitellut ristiriitaisuus selvitettyä: Lukion kemman oppikirja listaa elohopean hopeaa jalommaksi metallien sähkökemiallisessa jännitesarjassa, toisin kuin taulukkokirja(t). Tuohon ei liity mitään tilanne- tai tapauskohtaista tulkinnanvaraisuutta, vaan selvä virhe oppikirjassa ja hopea jalompi?
Pakko saada tämä vuosia kirjassa kummitellut ristiriitaisuus selvitettyä: Lukion kemman oppikirja listaa elohopean hopeaa jalommaksi metallien sähkökemiallisessa jännitesarjassa, toisin kuin taulukkokirja(t). Tuohon ei liity mitään tilanne- tai tapauskohtaista tulkinnanvaraisuutta, vaan selvä virhe oppikirjassa ja hopea jalompi?
muoks: Saman kirjasarjan toisessa myöhemmässä osassa, kun sähkökemiaa käsitellään uudelleen ja syvemmin, jännitesarjassa sama järjestys AG->HG.
muoks: Saman kirjasarjan toisessa myöhemmässä osassa, kun sähkökemiaa käsitellään uudelleen ja syvemmin, jännitesarjassa sama järjestys AG->HG.
Viimeksi muokattu:
Jaa vaikea sanoa. Elektronegatiivisuus (Paulingin asteikolla) Suomenkielisessä Wikipediassa:Tuohon ei liity mitään tilanne- tai tapauskohtaista tulkinnanvaraisuutta, vaan selvä virhe oppikirjassa ja hopea jalompi?
Elohopea 1,9
Hopea 1,93
(Järjestys vastaa taulukkokirjaa)
Englanninkielisessä Wikipediassa
Elohopea 2,00
Hopea 1,93
(Järjestys vastaa kemmankirjaa)
Eli selvästi järjestys vaihtuu riippuen lähteestä
Jaa vaikea sanoa. Elektronegatiivisuus (Paulingin asteikolla) Suomenkielisessä Wikipediassa:
Elohopea 1,9
Hopea 1,93
(Järjestys vastaa taulukkokirjaa)
Englanninkielisessä Wikipediassa
Elohopea 2,00
Hopea 1,93
(Järjestys vastaa kemmankirjaa)
Eli selvästi järjestys vaihtuu riippuen lähteestä
Vastaava tilanne näyttää olevan platinan ja kullan kanssa.
Esim. tämä näyttäisi olevan samoilla linjoilla taulukkokirjan kanssa järjestyksen osalta. Valitettavasti taulukossa käytetty luku (S) näyttäyisi olevan jollain muulla asteikoilla.
Mut siis ihan yleisesti asia ei välttämättä ole yksiselitteinen. Tässä esim. korrelaatio Sandersonin ja Paulungin elektronegatiivisuusasteikkojen välillä:
 en.wikipedia.org
en.wikipedia.org
Electronegativity - Wikipedia
Omassa lukion fyssan/kemian kirjasarjoissa ei taideta käsitellä esim. Daltonin osapainelakia tai osapaineasioita mitenkään, muuta kuin vain mainitsemalla ilmiö siellä täällä irrallisissa yhteyksissä. Tästä syystä esim. alla olevan maininnan merkitys jää itselleni epämääräiseksi (Esimerkki 3, vastauksen lopussa suluissa oleva huomio veden höyrynpainetta koskien). Ymmärrän asian niin, kuvan Hoffmannin kaasujen mittasäiliöihin muodostuu pieni määrä vesihöyrykaasua, mikä sisältyy alussa annettuun vetykaasun mitta-arvoon, mutta vähyyden vuoksi sitä ei tässä yhteydessä huomioida.
Tässä artikkelissa yritettiin laskea sen todennäköisyyttä, että kannattaako lipusta maksaa, vai ovatko tarkastukset tarpeeksi harvinaisia että pitkässäkin juoksussa pummilla selviää halvemmalla.
/img-s3.ilcdn.fi/e37236ebd8cf6c6ff5e2699cd06c3f1c18925fb08001cecd284fe52c9a5c926b.jpg)
 www.iltalehti.fi
www.iltalehti.fi
Kun tekee toistokokeen tuolla 0,83 prosentin todennäköisyydellä ja 121 yrityksellä, tulee ilman sakkoja selviämisen todennäköisyydeksi (onnistumiset = 0) 36,4 prosenttia. Kääntäen ainakin yhden tiketin saisi matkojen aikana "vasta" 63,5 prosentin todennäköisyydellä. Raja-arvo 50% todennäköisyydelle siitå että saa ainakin yhten tiketin näyttäisi menevän 84 matkan kohdalla. Toki tässäkin vedetään mutkia suoriksi, koska yhden matkan pituus voi vaihdella, ja pidemmällä matkalla on tietysti suurempi todennäköisyys jäädä kiinni.
Asian tutkimistahan voisi jatkaa vielä miettimällä, mikä on odotusarvo sille että yksittäisellä pummimatkalla säästää rahaa tai häviää rahaa.
/img-s3.ilcdn.fi/e37236ebd8cf6c6ff5e2699cd06c3f1c18925fb08001cecd284fe52c9a5c926b.jpg)
IL selvitti: Kannattaako HSL-alueella matkustaa pummilla? Matkan pituus ratkaisee
Vaikka todennäköisyys kohdata lipuntarkastajat on melko pieni, ovat paljon Helsingin sisällä matkustavien hyödyt liputta matkustamisesta vähäiset.
Eikös tässä ole nyt vedetty mutkia suoriksi? Eikö tätä pitäisi tutkia binomitodennäköisyyden ja toistokokeen avulla, jolla voitaisiin luoda malli siitä, että kuinka todennäköisesti kohdalle osuu 1 sakkolappu, 2 sakkolappua, 3 sakkolappua yms. tietyllä matkamäärällä? Tässä laskin, jos ei jaksa itse näpytellä laskimeen numeroita: Binomial CalculatorILTALEHTI sanoi:
- Tarkastuksen todennäköisyys saadaan, kun 3,3 miljoonaa tarkastusta jaetaan 397 miljoonalla matkalla. 3,3/397 = 0,0083 eli tarkastuksen todennäköisyys on 0,83 prosenttia.
- Se, miten monta matkaa voi matkustaa ennen kuin lippu tarkastetaan, lasketaan jakamalla sata lipuntarkastuksen todennäköisyydellä. 100/0,83 = 120,5 eli todennäköisyyksien mukaan 121. matkalla lippu tarkastetaan.
Kun tekee toistokokeen tuolla 0,83 prosentin todennäköisyydellä ja 121 yrityksellä, tulee ilman sakkoja selviämisen todennäköisyydeksi (onnistumiset = 0) 36,4 prosenttia. Kääntäen ainakin yhden tiketin saisi matkojen aikana "vasta" 63,5 prosentin todennäköisyydellä. Raja-arvo 50% todennäköisyydelle siitå että saa ainakin yhten tiketin näyttäisi menevän 84 matkan kohdalla. Toki tässäkin vedetään mutkia suoriksi, koska yhden matkan pituus voi vaihdella, ja pidemmällä matkalla on tietysti suurempi todennäköisyys jäädä kiinni.
Asian tutkimistahan voisi jatkaa vielä miettimällä, mikä on odotusarvo sille että yksittäisellä pummimatkalla säästää rahaa tai häviää rahaa.
- Liittynyt
- 02.11.2021
- Viestejä
- 132
Mitenkäs muuten nuo Gaussin ja Stokesin lauseet menevät kun dimensioita on > 3 ? Vektorien ristitulo taisi tuossa tapauksessa mennä vähän erilailla kuin 3D:ssä.
- Liittynyt
- 02.11.2021
- Viestejä
- 132
1x2=3 , 2x3=1 , 3x1=2 näin 3D:ssä mutta kun tulee enemmän dimensioita niin joutuu tekemään valintoja ja valinnoilla on taas seurauksia.
- Liittynyt
- 02.11.2021
- Viestejä
- 132
Mitenkäs muuten nuo Gaussin ja Stokesin lauseet menevät kun dimensioita on > 3 ? Vektorien ristitulo taisi tuossa tapauksessa mennä vähän erilailla kuin 3D:ssä.
Aiemmin pyörittelin tuota ideaa päässä niin 4D:ssä taisi käydä niin että Stokes tuli Gaussin tontille. Kynä-paperi-menetelmällä tuosta ei suurta ongelmaa tullut mutta jännä havainto. Osaisiko joku nimetä jotain kirjallisuutta aiheesta? Väisälän vektorialgebra ja SimoK:n analyysit ovat jo tuttuja.
Uutiset
-
Intel julkaisi pitkään huhutun pelkkiä P-ytimiä sisältävän Bartlett Laken
10.3.2026 01:15
-
Uusi artikkeli & video: Testissä Google Pixel 10a
9.3.2026 16:55
-
Uusi artikkeli: Testissä Sony WF-1000XM6 -nappikuulokkeet
9.3.2026 14:42
-
Intel julkaisi uudet Xeon 6+ -prosessorit ja herätti samalla ulkopuolisen kiinnostuksen Intel 18A -prosessiin
6.3.2026 14:34
-
Google esitteli maaliskuun Pixel Dropissa uusia ominaisuuksia omille Pixel-puhelimilleen
6.3.2026 13:35

