Kysyin tuolta Pieniä kysymyksiä ohjelmoinnista apua seuraavaan pulmaan:
Mutta tämä ehkä parempi paikka.
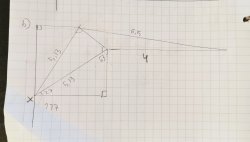
Miten lasketaan pisteen ja kolmion välinen etäisyys, eli miten valitaan monen kolmion seasta se lähin?
Olen koittanut tuota ratkoa laskemalla jokaisesta kolmiosta janan ja pisteen välisen suorakulmaisen etäisyyden ja valitsemalla sen kolmion, jossa on etäisyys pienin. Tämä ei toimi kuten kuvasta voi päätellä.
Pisteen suorakulmainen etäisyyys on oranssista kolmiosta pienempi kuin sinisen, vaikka sininen kolmio on lähempänä.