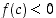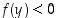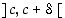15km/L on tietysti 7,5L/100km HÄH paitsi ei olekkaan (100/15) = 6,67L/100km
Aivot vielä jumissa eli mitenkäs se 20km/L ja 10km/L puoliväli ei olekkaan 7,5?
Käänteisarvojen keskiarvo (1/a+1/b)/2 ei ole sama kuin keskiarvojen käänteisarvo 1/(a/2+b/2)
Tuossa olet siis nimenomaan laskenut keskiarvoja, et "puoliväliä". Puolivälin arvo riippuu käyrästä.
Jos haluat korvata rinnakkain laitetut 2kΩ ja 1kΩ vastukset kahdella samanarvoisella, niin siihen ei laiteta kahta 1,5kΩ vastusta vaan kaksi ~1,33kΩ vastusta.
( 1/2 + 1/1 ) ≈ ( 1/1,33 + 1/1,33 )
Viimeksi muokattu:

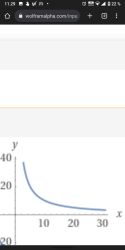



 Auttakee tyhmää!
Auttakee tyhmää!