Säästäminen ja sijoittaminen (osakkeet, rahastot, ETF:t...)

[Clarenz]

Itse pyrkisin kurssien putoamisen yhteydessä ostamaan vasta avattuun OST:n hyvä kotimaisia osinkolappuja ja AOT:lle isoja kansainvälisiä firmoja, kuten esim Applea. Toki normi kk-säästöt saisi rullata, kun sitä ei koskaan tiedä ollaanko pohjalla vai vieläkö tippuu.

 

[Nomber]

Hypoteettinen kysymys: jos se kauan ennustettu ja paljon puhuttu romahdus nyt lähiaikoina iskisi, mitä lähtisitte sitten sieltä alelaarin pohjalta haalimaan? En nyt siis hae mitään hirveän spesifiä, vaan lähinnä sellaisia yleisluontoisempia ajatuksia/lähestysmistapoja. Pelkästään osakkeita, vai myös esim. ETF:iä ja muita instrumentteja? Ylipäätään ale-osakkeiden haalimisen taustalla pitää tietysti olla usko siihen, että ne ponnistavat sieltä pohjalta takaisin ylös. Näinhän ei suinkaan aina käy ja varsinkin tosi isoissa laskuissa menee välillä isojakin firmoja nurin ja selviytyjistäkään kaikki eivät ikinä kunnolla toivu kun luovan tuhon markkinoille ponnistaa uusia, vähän dynaamisempia firmoja ilman menneisyyden painolastia jne. Toisaalta kaikkein vakavaraisimpien ja isoimpien toimijoiden (tyyliin Alphabet, Apple jne.) osakkeet eivät välttämättä niin paljoa edes dippaa.

Ihan samoja ETF:iä ja rahastoja kuin nytkin. Miksi muuttaa mitään? Jos oikein rommaa paljon niin ehkä nostaisin kk säästösummaa isommaksi joksikin aikaa niin pääsisi eroon liiallisesta käteisestä jota on päässyt kertymään. En osaa valita mitään osaketta oikein enkä ajoittaa ostoa oikein, joten menen loppuun asti samalla strategialla ostamalla säännöllisesti hajautettuja ETF:iä joissa on mahdollisimman piene kulut. En harrasta myöskään lottoamista vaan laitan siitäkin säästyneet rahat ETF:iin. Uskon vahvasti että tämä on kymmenien vuosien aikajänteellä voittava strategia.

 

[zepi]

Itse pistin äsken Nvidiaa ja AMD:tä laitaan ja meinasin ostaa tylsästi vain IWDA:aa tilalle. Nvidia possa on +1600% ja aivan liian isolla painolla salkussa ja AMD:kin vaivaiset +1100%.

Ja Sveitsissä kun asun, niin myyntivoittoveroja ei tarvitse maksaa, kunhan ei harrasta day treidausta -> helppoa päätös tehdä pieniä allokaatiomuutoksia ja laskea salkun riskitasoa kun minulla on näkemystä sen suhteen, että kryptobuumi saattaa olla viimein vähän lässähtämässä ja se saattaa näkyä näytönohjainten kysyntää vähentävänä tekijänä.

 

[xylitoli]

Hypoteettinen kysymys: jos se kauan ennustettu ja paljon puhuttu romahdus nyt lähiaikoina iskisi, mitä lähtisitte sitten sieltä alelaarin pohjalta haalimaan?

Omalta osaltani riippuisi siitä että onko romahduksella sellainen syy, jonka vuoksi jonkun tietyn sektorin arvopapereihin ei ehdottomasti kannattaisi sijoittaa tai johonkin toiseen ehdottomasti kannattaisi vai onko kyseessä markkinan perinteinen ylireagointi. Tuollainen muu syy kuin pelkkä yliragointi, saisi poikkeamaan normaalista ostoslistastani. Ylläpidän siis lyhyttä ostoslistaa siitä mitä salkkuihin voisi seuraavaksi hankkia, jos markkina sattuisi hinnoittelemaan hetkellisesti väärin.

 

[stool]

Se on jotenkin huvittavaa, että valtaosa sijoittajista myöntää ajoittamisen olevan mahdotonta, mutta silti valtaosa samoista henkilöistä sitä harrastaa. Eli siis jemmaa käteiskassaa, säätää kuukausisummaa yms. pientä venkslausta. Eipä sitä varmaan mielletä niin aktiiviseksi toiminnaksi, mutta yhtä lailla siinä otetaan näkemystä sen puolesta, että ollaan itse markkinaa fiksumpia.

 

[dropadrop]

Ei kai sitä ihminen itselleen mitään voi. Pitäisi jättää kirjautumatta palveluihin jos haluisi olla kokonaan venkslaamatta.

 

[Lammas]

[...] kryptobuumi saattaa olla viimein vähän lässähtämässä ja se saattaa näkyä näytönohjainten kysyntää vähentävänä tekijänä.

Onko mitään tietoa kuinka iso rooli kryptoilla on nykyään näyttismarkkinoilla? Ei olisi tullut mieleenkään ajatella asiaa noin, mutta mulla ei toisaalta ole mitään kryptokokemusta, niin ehkä aliarvioin niiden vaikutuksen mihinkään nykymaailmassa.

 

[Lammas]

Jep, nasdaq on ollut laskussa marraskuun huipusta tällepäivää luokkaa 10%. Eli sen suunta keskimäärin on ollut siis reilun 1kk laskeva. Helppoa todeta näin takautuvasti. Se mikä on vaikeampaa on todeta mitä tapahtuu huomenna yksittäisen osakkeen kurssille.

Ylläoleva kommenttini saattaa kuulostaa itsestään selvyydeltä. Siksi pitää myös huomioida se seikka että tilastojen mukaan suunnan jatkuminen on todennäköisempää kuin sen kääntyminen. Tämä ei ole uskon asia, vaan jokainen voi tarkistaa asian excelillä tai muulla sopivalla välineellä. Kohina, eli päivittäinen heilunta kannattaa suodattaa pois, niin tilannekuva käy selvemmäksi. Yksinkertaisia suodattimia kohinanpoistoon, joilla kylläkin myöhästyy suunnan käänteestä jonkin verran, ovat indexistä liukuva keskiarvo(50), ja exponentiaalinen liukuva keskiarvo(50). Paljon kehittyneempiäkin systeemejä suunnan todennäköisyyden arviointiin löytyy.

Tietenkään pelkästä indexikehityksestä/suunnasta ei pitäisi pysytyä näkemään ennakolta yllättäviä luonnonkatastrofeja, joten niiden ja vastaavien aiheuttamat äkilliset suunnanmuutokset eivät lähtökohtaisesti ole ennustettavissa pelkästä indexi-datasta.

Jos joku sanoo ettei edellisten päivien kurssikehityksellä ole mitään ennustearvoa huomisen kursseille, niin hän esittää väitteen että jokaisen päivän kurssikehitys on täysin satunnaista ja irrallaan reaalimailman tapahtumista, niin kuin se olisi nopalla heittämistä tai rulettia. Mikään olemassaoleva osakekaupankäyntitilasto indexitasolla ei tue sellaista väitettä.

Todellisuudessa kurssikehitys indexitasolla on lähempänä öljytankkerin liikkumista merellä - suuren massansa takia se ei ole seuraavana päivänä planeetan toisella puolella, tai esitä delffiinin kaltaisia flippejä, tai vedä luistimia jalkaan. Muistetaan kuitenkin että tankkeri voi ajaa karille, tai se joutuu normaalista poiketen odottelemaan satamaan pääsyä, mutta nämä eivät ole sääntö vaan poikkeus.

(lihavoin oleelliset kohdat)
Olisin kiinnostunut kuulemaan lisää noista tilastoista ja excel-taulukoista, jotka osoittavat trendien, varsinkin laskevien sellaisten, olemassaolon. Millaisella matemaattisella mallilla mallinnat kurssien tai indeksien kehitystä? Itse olen käyttänyt vain geometrista Brownin liikettä, joka tietääkseni on varsin yleisesti käytetty, mutta joka ei tue noita mainitsemiasi ominaisuuksia. Tai no tarkalleen ottaen jos käyttää positiivista driftiä, niin silloinhan on yksi suunta, ylöspäin, joka on aina todennäköisempi kuin muut suunnat. Tällöin myös suunnan jatkuminen on käytännössä todennäköisempää kuin sen kääntyminen, määrittelipä "suunnan" miten tahansa. Mutta tämä tieto on täsmälleen yhtä hyödyllinen kuin se, että keskimäärin ostaminen kannattaa aina.

 

[FinMaky]

Onko mitään tietoa kuinka iso rooli kryptoilla on nykyään näyttismarkkinoilla? Ei olisi tullut mieleenkään ajatella asiaa noin, mutta mulla ei toisaalta ole mitään kryptokokemusta, niin ehkä aliarvioin niiden vaikutuksen mihinkään nykymaailmassa.

Todella merkittävä. Q1 2021 25% näytönohjaimista myytiin kryptolouhintaan (googlefu löysi nopeiten tuon ajankohdan). Samaan aikaan oli komponettipula, josta johtuen näytönohjainten hinnat oli ja on ihan pilvissä, joten enemmän olisi varmaan myyty, jos ohjaimet olisi "normaalihintaisia", koska louhinta on business. Mä en näe että tänävuonna näytönohjainten hinta normalisoituisi. Ehkä ensivuonna aikaisintaan. Ja sekin vaatii sitä että kryptomainaus vähenee reilusti, mikä näyttää mahdolliselta. Tuossa käytössä alkaa 3v kohdalla näytönohjaimet hajoamaan, toki voi kestää pidempään, mutta 5v käyttöikää enempää en ainakaan itse odottaisi, joten uusintatarve on jatkuva. Ja sitten jos hinnat alkavat normalisoitua menee vuosi tai pari että patoutunut kysyntä kuluttajapuolelta saadaan katettua. Monella näytönohjainpäivitys odottaa että hinnat tippuu järjelliselle tasolle. Esimerkki minä. Ostin GTX1070ti 11.10.2018 hintaan 333€, samalaisten korttien hinta ollut koko viimevuoden 699€, eli voisin onnistua myydä tuon vieläkin voitolla pois! Heti kun hinnat tippuu että saan paremman kortin about samaan ostohintaan, niin vaihtoon lähtee, mutta en toisiaan usko ennen 23 black fridayta tuota tapahtuvan.

 

[xylitoli]

(lihavoin oleelliset kohdat)
Olisin kiinnostunut kuulemaan lisää noista tilastoista ja excel-taulukoista, jotka osoittavat trendien, varsinkin laskevien sellaisten, olemassaolon. Millaisella matemaattisella mallilla mallinnat kurssien tai indeksien kehitystä? Itse olen käyttänyt vain geometrista Brownin liikettä, joka tietääkseni on varsin yleisesti käytetty, mutta joka ei tue noita mainitsemiasi ominaisuuksia. Tai no tarkalleen ottaen jos käyttää positiivista driftiä, niin silloinhan on yksi suunta, ylöspäin, joka on aina todennäköisempi kuin muut suunnat. Tällöin myös suunnan jatkuminen on käytännössä todennäköisempää kuin sen kääntyminen, määrittelipä "suunnan" miten tahansa. Mutta tämä tieto on täsmälleen yhtä hyödyllinen kuin se, että keskimäärin ostaminen kannattaa aina.

Kerrot käyttäväsi geometrista Brownin liikettä mallintamiseen. Pyritkö siis löytämään sillä indeksitason trendiä joltain tietyltä aikaväliltä, vaiko mitä? Mielestäni olisi erikoista, että teoreema joka on johdettu hiukkasten satunnaisen lämpöliikkeen aiheuttaman liikkeen kuvaamiseen, voisi toimia kovinkaan hyvin ennustamaan ei satunnaisia ilmiöitä kuten hinnan muodostuminen yhteen suuntaan etenevässä aikasarjassa indexitasolla.
Jos oikein luen niin itsekkin toteat ettei sillä löydy trendien olemassaoloa. Jos näin olet havainnut, niin silloin olet tavallaan todistanut että random walkiin perustuvat medotit eivät sovellu trendien havainnointiin osakeindekseistä ja/tai kuten myös todellisuudessa on että kyseisten indexien hinnanmuodostus ei perustu satunnaisuuteen. Varmuuden vuoksi, ettei tästä tule vääriä johtopäätöksiä, mitä käytit syöttödatana ja miten sovelsit Brownin liikettä siihen?

Lainaamassasi tekstissä kerron että trendit löytyvät jo niinkin yksinkertaisilla välineillä kuin liukuvilla keskiarvoilla. Jos käytät yhtäaikaisesti useampaa liukuvaa keskiarvo eri periodimäärillä, esim 20, 35, 50, 75, 200. Niin kaikkien mainittujen keskiarvojen noustessa trendi on nouseva, tai kaikkien mainittujen keskiarvojen laskiessa päivittäin trendi on alas. Silloin kun lyhemmän keskiarvon piirtämä käyrä leikkaa pidemmän keskiarvon piirtämää käyrää, kyseessä on tilanne että trendi on mahdollisesti kääntymässä. Näin yksinkertaistettuna. Kuitenkin todellisuudessa indexin aikasarja muodostuu useista eri toimijoiden ja vaikuttavien tekijöiden aikaansaamista osa trendeistä, joilla ei ole keskenään sama jakson mitta. Joten jos olet tekemässä tästä jotain tieteellistä tutkimusta, niin jollain Fourier tai muulla vastaavalla menetelmällä kannattaa ajaa lähtödata ja katsoa minkä mittaisia jaksoja sieltä löytyy ja erotella ne omiksi komponenteikseen trendi ilmaisimille. En tiedä miten pitkään ja mitä menetelmiä olet yrittänyt soveltaa trendin ilmaisuun, mutta varmuuden vuoksi kannattaa pitää systeemit suht yksinkertaisina ja tutustua vaikka Wildersin ajatuksiin. Jos taas ajattelit tienata näillä niin sitten kannattaa tutkia vaikka tekoälyn soveltamista yhdistettynä geneettisiin perimään parhaimmin onnistuvien tekoälyjen seuraavin generaatioiden muodostumiseen ja jättää algoritmin keksiminen tekoälyn/neuroverkon sisäiseksi asiaksi.

Edit: Tässä näemmä joku on kasannut ihan paperin, joka vastaa pitkälle omia havaintojani: https://irep.ntu.ac.uk/id/eprint/32787/1/PubSub10294_702a_McGinnity.pdf

Jos ei muuta jaksa kahlata läpi, niin sivulta 23 Table V. Todennäköisyydet hyvällä medotilla oikein valituilla aikaikkunoilla ovat >50%. Ts. korrelaatio on olemassa.

Edit 2. Tuli mieleen yleisesti että jos käyttämäsi menetelmä ei löydä niitä lyhyitä laskevia trendejä pitkäaikaisen nousevan trendistön seasta, niin ehkä menetelmäsi vaatisi dataan ennakolta "skew" korjauksen, joka nollaa pitkäaikaisen perustrendin (sen joka on indexeille se jotain 7% / vuosi kun tarkastellaan tosi pitkiä aikoja)?

 

[zepi]

Todella merkittävä. Q1 2021 25% näytönohjaimista myytiin kryptolouhintaan (googlefu löysi nopeiten tuon ajankohdan). Samaan aikaan oli komponettipula, josta johtuen näytönohjainten hinnat oli ja on ihan pilvissä, joten enemmän olisi varmaan myyty, jos ohjaimet olisi "normaalihintaisia", koska louhinta on business. Mä en näe että tänävuonna näytönohjainten hinta normalisoituisi. Ehkä ensivuonna aikaisintaan. Ja sekin vaatii sitä että kryptomainaus vähenee reilusti, mikä näyttää mahdolliselta. Tuossa käytössä alkaa 3v kohdalla näytönohjaimet hajoamaan, toki voi kestää pidempään, mutta 5v käyttöikää enempää en ainakaan itse odottaisi, joten uusintatarve on jatkuva. Ja sitten jos hinnat alkavat normalisoitua menee vuosi tai pari että patoutunut kysyntä kuluttajapuolelta saadaan katettua. Monella näytönohjainpäivitys odottaa että hinnat tippuu järjelliselle tasolle. Esimerkki minä. Ostin GTX1070ti 11.10.2018 hintaan 333€, samalaisten korttien hinta ollut koko viimevuoden 699€, eli voisin onnistua myydä tuon vieläkin voitolla pois! Heti kun hinnat tippuu että saan paremman kortin about samaan ostohintaan, niin vaihtoon lähtee, mutta en toisiaan usko ennen 23 black fridayta tuota tapahtuvan.

Eikä pelkästään se uusien korttien menekki vaan myös se, että jos cryptojen mainaus vähenee, niin käytettyjä kortteja valuu myyntiin samalla kun kysyntä laskee.

Ethereumin kurssi on nyt pudonnut ~€4000/ETH tasolta ~€2800/ETH tasolle, joten pelkästään tuo vähentää näyttismainauksen kannattavuutta aika paljon.

 

[Clarenz]

Eikä pelkästään se uusien korttien menekki vaan myös se, että jos cryptojen mainaus vähenee, niin käytettyjä kortteja valuu myyntiin samalla kun kysyntä laskee.

Ethereumin kurssi on nyt pudonnut ~€4000/ETH tasolta ~€2800/ETH tasolle, joten pelkästään tuo vähentää näyttismainauksen kannattavuutta aika paljon.

Toisaalta olihan Ethereum viime kesällä merkittävästi halvempi (pitkään alle 2000€, halvimmillaan 1500€)vielä ja silti ei niitä kortteja missään kai mahottomasti ollut myynnissä?

mutta tokihan Nvidian ja AMD:n arvostukset ovat kovat.

 

[xylitoli]

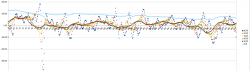
@Lammas Ohessa kuvaaja excelistä, jossa OMHEX-PI indexin 600 menneen viikon osalta alkeellinen regressio menetelmä ilmaisee trendit. Lukuohje: Vasen reuna on nykyhetki, ja menneet viikot jatkuvat oikealle, niin että oikea reuna on jossain kymmenen vuotta sitten.
Vaaleansininen on Hexin viikkokäyrä, joka on skaalattu jakamalla sadalla että mahtuu nätisti ilmaistujen trendien kanssa samaan kuvaan.
Ruskea käppyrä ilmaisee hitaita trendejä, luokkaa vuositaso, tummansininen nopeampia, luokkaa 2kk. Ja muut siltä väliltä. Trendi on nouseva jos sitä kuvaava käppyrä on X-akselin yläpuolella, ja Trendi on laskeva jos se on X-akselin alapuolella jne. Kuvaajasta nähdään että viimeisen kymmenen vuoden aikana pidempi "vuositason" trendi on ollut laskeva neljästi. Tämä ei ole mitenkään optimoitu ja kohdilleen säädetty, mutta laitoin siksi että olipa käytetty trendin ilmaisu menettely mikä tahansa, niin jos se toimii, ja puhutaan vuositason ilmiöistä, niin sen pitäisi siis löytää samat 4 laskevan trendin ajanjaksoa. Jos ei löydä, niin jossain on virhe. (Ja nyt en tarkoita sitä että millä ajanhetkellä mikäkin algoritmi kykenee huomaamaan trendin käännöksen, oheisesta kuvaajastahan näkee että samakin algoritmi antaa eri tuloksia riippuen sen käyttämästä aikaikkunasta.

Muille lukijoille pahoittelut, että tässä aletaan olemaan jo varsin kaukana ketjun aiheesta säästäminen... Mutta on tällä se liittymäkohta että treidaus roboteilla on ihan pätevät algoritmit joilla päästään keskimäärin yli 75% oikeaan osuviin arvioihin siitä mihin suuntaan markkina liikkuu. Tuossa kuvassa ei siis ole käytetty mitenkään erityisen hyvää algoritmiä, se on perus regression soveltamista.

 

[xylitoli]

Puttonen avaa mielenkiintoisia näkökantoja inflaatiosta ja korkotilanteesta artikkelissa joka on julkaistu Arvopaperissa 7.1. Valitettavasti maksumuurin takana, mutta joku on mennyt postaamaan sen niin että näkyy tällä ylimmäisenä Vahva osta Nokialle Q1/2022 | Kauppalehti.fi

"Uskon, ettei koronnostoja tule. Keskuspankeilla on nyt suurempi paine hyväksyä alhaiset nimelliskorot ja aiempaa korkeampi inflaatio kuin lähteä nostamaan ohjauskorkoa."

ja

Keskuspankkien nykylinjan jatkaminen tarkoittaa Puttosen mukaan sitä, että ne joilla on osakkeita, kiinteistöjä, metsää tai muuta reaaliomaisuutta, vaurastuvat edelleen.

 

[Lammas]

Kerrot käyttäväsi geometrista Brownin liikettä mallintamiseen. Pyritkö siis löytämään sillä indeksitason trendiä joltain tietyltä aikaväliltä, vaiko mitä? Mielestäni olisi erikoista, että teoreema joka on johdettu hiukkasten satunnaisen lämpöliikkeen aiheuttaman liikkeen kuvaamiseen, voisi toimia kovinkaan hyvin ennustamaan ei satunnaisia ilmiöitä kuten hinnan muodostuminen yhteen suuntaan etenevässä aikasarjassa indexitasolla.
Jos oikein luen niin itsekkin toteat ettei sillä löydy trendien olemassaoloa. Jos näin olet havainnut, niin silloin olet tavallaan todistanut että random walkiin perustuvat medotit eivät sovellu trendien havainnointiin osakeindekseistä ja/tai kuten myös todellisuudessa on että kyseisten indexien hinnanmuodostus ei perustu satunnaisuuteen. Varmuuden vuoksi, ettei tästä tule vääriä johtopäätöksiä, mitä käytit syöttödatana ja miten sovelsit Brownin liikettä siihen?

Lainaamassasi tekstissä kerron että trendit löytyvät jo niinkin yksinkertaisilla välineillä kuin liukuvilla keskiarvoilla. Jos käytät yhtäaikaisesti useampaa liukuvaa keskiarvo eri periodimäärillä, esim 20, 35, 50, 75, 200. Niin kaikkien mainittujen keskiarvojen noustessa trendi on nouseva, tai kaikkien mainittujen keskiarvojen laskiessa päivittäin trendi on alas. Silloin kun lyhemmän keskiarvon piirtämä käyrä leikkaa pidemmän keskiarvon piirtämää käyrää, kyseessä on tilanne että trendi on mahdollisesti kääntymässä. Näin yksinkertaistettuna. Kuitenkin todellisuudessa indexin aikasarja muodostuu useista eri toimijoiden ja vaikuttavien tekijöiden aikaansaamista osa trendeistä, joilla ei ole keskenään sama jakson mitta. Joten jos olet tekemässä tästä jotain tieteellistä tutkimusta, niin jollain Fourier tai muulla vastaavalla menetelmällä kannattaa ajaa lähtödata ja katsoa minkä mittaisia jaksoja sieltä löytyy ja erotella ne omiksi komponenteikseen trendi ilmaisimille. En tiedä miten pitkään ja mitä menetelmiä olet yrittänyt soveltaa trendin ilmaisuun, mutta varmuuden vuoksi kannattaa pitää systeemit suht yksinkertaisina ja tutustua vaikka Wildersin ajatuksiin. Jos taas ajattelit tienata näillä niin sitten kannattaa tutkia vaikka tekoälyn soveltamista yhdistettynä geneettisiin perimään parhaimmin onnistuvien tekoälyjen seuraavin generaatioiden muodostumiseen ja jättää algoritmin keksiminen tekoälyn/neuroverkon sisäiseksi asiaksi.

Edit: Tässä näemmä joku on kasannut ihan paperin, joka vastaa pitkälle omia havaintojani: https://irep.ntu.ac.uk/id/eprint/32787/1/PubSub10294_702a_McGinnity.pdf

Jos ei muuta jaksa kahlata läpi, niin sivulta 23 Table V. Todennäköisyydet hyvällä medotilla oikein valituilla aikaikkunoilla ovat >50%. Ts. korrelaatio on olemassa.

Edit 2. Tuli mieleen yleisesti että jos käyttämäsi menetelmä ei löydä niitä lyhyitä laskevia trendejä pitkäaikaisen nousevan trendistön seasta, niin ehkä menetelmäsi vaatisi dataan ennakolta "skew" korjauksen, joka nollaa pitkäaikaisen perustrendin (sen joka on indexeille se jotain 7% / vuosi kun tarkastellaan tosi pitkiä aikoja)?

Pääasiallisena tarkoituksena mulla on mallintaa sijoitusten kehitystä pitkällä aikavälillä ja vastata kysymyksiin kuten: "kuinka paljon pitää säästää viikossa, jotta vuonna X omaisuutta on todennäköisyydellä 90% vähintään Y euroa?" Tässä yhteydessä minulla on tapana olettaa, että valitut arvopaperit (yksinkertaisimmillaan esim. yksittäinen indeksiä seuraava ETF) noudattavat geometrista Brownin liikettä valituilla kiinteillä parametreilla. Mutta jos onkin niin, kuten väität, että indeksit "seuraa suuntaa", niin silloin käyttämäni malli on väärä ja saan väärät tulokset eläköitymislaskelmistani. (Toki saan väärät tulokset siinäkin tapauksessa että indeksi noudattaa täsmälleen geometrista Brownin liikettä, mutta parametreilla, joita en tarkkaan tunne.) Mutta mallin käyttötarkoitus on oikeastaan sivuseikka. Jos tietäisin jonkun tosi hyvän mallin, niin voisinhan mä kokeilla sitä vaikka ostojen ajoittamiseen. Yritin muutama vuosi sitten etsiä jotain hyväksi todettuja malleja, mutta en löytänyt juuri mitään, mutta ehkä mulla oli väärä hakusanat, kun alan termistö on aika hukassa.

@Lammas Ohessa kuvaaja excelistä, jossa OMHEX-PI indexin 600 menneen viikon osalta alkeellinen regressio menetelmä ilmaisee trendit. Lukuohje: Vasen reuna on nykyhetki, ja menneet viikot jatkuvat oikealle, niin että oikea reuna on jossain kymmenen vuotta sitten.
Vaaleansininen on Hexin viikkokäyrä, joka on skaalattu jakamalla sadalla että mahtuu nätisti ilmaistujen trendien kanssa samaan kuvaan.
Ruskea käppyrä ilmaisee hitaita trendejä, luokkaa vuositaso, tummansininen nopeampia, luokkaa 2kk. Ja muut siltä väliltä. Trendi on nouseva jos sitä kuvaava käppyrä on X-akselin yläpuolella, ja Trendi on laskeva jos se on X-akselin alapuolella jne. Kuvaajasta nähdään että viimeisen kymmenen vuoden aikana pidempi "vuositason" trendi on ollut laskeva neljästi. Tämä ei ole mitenkään optimoitu ja kohdilleen säädetty, mutta laitoin siksi että olipa käytetty trendin ilmaisu menettely mikä tahansa, niin jos se toimii, ja puhutaan vuositason ilmiöistä, niin sen pitäisi siis löytää samat 4 laskevan trendin ajanjaksoa. Jos ei löydä, niin jossain on virhe. (Ja nyt en tarkoita sitä että millä ajanhetkellä mikäkin algoritmi kykenee huomaamaan trendin käännöksen, oheisesta kuvaajastahan näkee että samakin algoritmi antaa eri tuloksia riippuen sen käyttämästä aikaikkunasta.

Muille lukijoille pahoittelut, että tässä aletaan olemaan jo varsin kaukana ketjun aiheesta säästäminen... Mutta on tällä se liittymäkohta että treidaus roboteilla on ihan pätevät algoritmit joilla päästään keskimäärin yli 75% oikeaan osuviin arvioihin siitä mihin suuntaan markkina liikkuu. Tuossa kuvassa ei siis ole käytetty mitenkään erityisen hyvää algoritmiä, se on perus regression soveltamista.

Tuostakaan kuvaajasta ei kyllä heti käy ilmi, että mikä siinä on ristiriidassa Brownin liikkeeseen perustuvan kurssikehityksen kanssa. Kyllähän melkein mistä tahansa satunnaiskävelystä voi löytää erilaisia jaksoja jolloin mennään ylös tai alas, mutta tulevaisuus näyttää joka kohdassa silti ihan samalla tavalla jakautuneelta.

 

[elmo]

Puttonen avaa mielenkiintoisia näkökantoja inflaatiosta ja korkotilanteesta artikkelissa joka on julkaistu Arvopaperissa 7.1. Valitettavasti maksumuurin takana, mutta joku on mennyt postaamaan sen niin että näkyy tällä ylimmäisenä Vahva osta Nokialle Q1/2022 | Kauppalehti.fi

"Uskon, ettei koronnostoja tule. Keskuspankeilla on nyt suurempi paine hyväksyä alhaiset nimelliskorot ja aiempaa korkeampi inflaatio kuin lähteä nostamaan ohjauskorkoa."

ja

Keskuspankkien nykylinjan jatkaminen tarkoittaa Puttosen mukaan sitä, että ne joilla on osakkeita, kiinteistöjä, metsää tai muuta reaaliomaisuutta, vaurastuvat edelleen.

Ihan asiaahan tuo puhuu siitä, että velkaa on niin paljon ettei korkojen nosto onnistu. Onhan se vähä naurettavaa, että pankit stressitestaa 5% korkotasolla asuntolainanottajia, mutta sitten isot pelurit jotka ottaa sellasia lukemia velkaa jota tavan tallaaja ei edes ymmärrä ei tule kestämään edes puolta tuosta. Mielenkiinnolla odotetaan mitä keksivät... Todennäköisesti jotain millä massat maksaa persaukisten jättivelkaisten nousevat korot jossain muodossa jos nosto linjalle lähdetään korkojen suhteen.

Jatkan samaa kuukausi säästöä kun en osaa ennustaa. Summa tuli tuplattua koronan alkaessa 500->1000€ ja siellä saa olla vieläkin. Jos jää jotain euroja tuosta yli niin ne menee crypto leikkeihin. Käteistä en viitsi kerätä kun ei sille ole mitään tarvetta. En osaa hyödyntää mitään ostopaikkoja ja jos taloudellinne kurjimus (työttömyys) iskisi omalle kohdalle niin selviäisin luottokorteilla sen puolen vuotta kevyesti tai sitten koskisi sijoituksiin kumpi ennemmin kannattaakin. Aluksi hillosin puolen vuodennetto palkkaa mikä nyt oli ihan tyhmää.

 

[tuoppi´]

Ihan asiaahan tuo puhuu siitä, että velkaa on niin paljon ettei korkojen nosto onnistu. Onhan se vähä naurettavaa, että pankit stressitestaa 5% korkotasolla asuntolainanottajia, mutta sitten isot pelurit jotka ottaa sellasia lukemia velkaa jota tavan tallaaja ei edes ymmärrä ei tule kestämään edes puolta tuosta. Mielenkiinnolla odotetaan mitä keksivät... Todennäköisesti jotain millä massat maksaa persaukisten jättivelkaisten nousevat korot jossain muodossa jos nosto linjalle lähdetään korkojen suhteen.

Jep, tässä on maailma ajettu siihen tilanteeseen että kumpikin vaihtoehdoista on todella huono. Joko annettava inflaation laukata vapaasti ja talous kaatuu siihen tai sitten nostettava korkoja reilusti ja talous kaatuu siihen. Oikeastaan kysymys ei enää ole että kaatuuko talous vaan että kuinka pahasti.

 

[Aatos]

Tuosta "totuutena toistetusta" korkoja ei voi nostaa-mantrasta oma mielipiteeni on se, että ei ne EKP:n teknokraatit mitään kaikkivoipia jumalia ole.

Todennäköisesti asiat varmaan etenevätkin kuten ennustettu, mutta aina voi tulla yllättävä käänne kuten esimerkiksi populistien valtaannousu Saksassa tai Ranskassa joka sotkee logiikkaan perustuvan tapahtumien kulun. Tämän riskin kokoa voi sitten itse kukin pohtia.

 

[xylitoli]

Pääasiallisena tarkoituksena mulla on mallintaa sijoitusten kehitystä pitkällä aikavälillä ja vastata kysymyksiin kuten: "kuinka paljon pitää säästää viikossa, jotta vuonna X omaisuutta on todennäköisyydellä 90% vähintään Y euroa?" ... Yritin muutama vuosi sitten etsiä jotain hyväksi todettuja malleja, mutta en löytänyt juuri mitään, mutta ehkä mulla oli väärä hakusanat, kun alan termistö on aika hukassa.

OK. Erittäin hyvä tavoite. Voi olla että parhaillakaan kaavoilla ei saisi luotettavaa tulosta. Siksi aika usein päädytään siihen että tehdään eri skenaarioita kurssikehityksestä, ja katsotaan millaisia lopputuloksia syntyy. Esim voit laittaa tietokoneen arpomaan sinulle satoja (tuhansia) erilaisia versioita jotka ovat pseudosamankaltaisia kuin kohteena olleen Etf:n tai paremminkin sen edustaman indexin kanssa. Varioiden esim keskimääräistä nousukulmaa, ja nousujaksojen sekä laskujaksojen suhteellisia osuuksia toisiinsa nähden. Ja seurata miten ennusteet eri varianteilla konvertoituvat tai hajaantuvat.

Mitä pidemmälle tulevaisuuteen simuloit sitä varmemmin ennusteen luotettavuus heikenee. Nimittäin vaikka edeltävän jo toteutuneen laajan indexin kurssikehityksen perusteella voidaan ennustaa vähintään 75% todennäköisyydellä tulevaa kurssikehitystä, niin ne parhaat ennustetodennäköisyydet koskevat vain välitöntä lähitulevaisuutta. Pidemmällä aikavälillä ulkoiset tekijät käyvät dominanteiksi, kuten tuleeko vai ei 5. ja 6. teollinen vallankumous, hyperinflaatio, suursota, ylittääkö väestönkasvu planeetan elintarviketuotantokyvyn jne. Pitkällä ajalla ennustamisen haasteet ovat siis niitä samoja joita käsitelläään kaaosteorian puolella.

Tuottavuuden, markkinan kasvu (tuotevalikoiman laajentuminen, väestönklasvu ym.), ovat niitä tekijöitä jotka aiheuttavat kursseille sen "perusnosteen" joka on vallinnut pitkään. Ja Kysyntä/tarjonta, Ahneus/pelko, ym satunnaiset tapahtumat aiheuttavat niitä häiriöitä joilden vuoksi päivittäinen osakekurssi poikkeaa, eli heilahtaa pois kulloinkin "perusnosteesta" mutta pyrkii aikaa myöten palaamaan siihen-->Tästä voi tehdä mallin, mutta edelleenkään epävarmuus lopputuloksesta ei poistu.

Parhaat kaupankäyntialgoritmit eivät ole julkisia, mutta opensource puoleltakin löytyy satoja projekteja kahlattavaksi:

The Top 309 Trading Algorithms Open Source Projects

Browse The Most Popular 309 Trading Algorithms Open Source Projects

awesomeopensource.com

Itselleni on ollut hyötyä sentyyppisistä joissa useampi algoritmi "äänestää" oman näkemyksensä ja sitten sijoittajana itse viimekädessä pohdin ja päätän miksi ne ovat päätyneet ko tulokseen ja voinko pitää tulosta kulloinkin kuinka perusteltuna ja toiminko sen mukaan vai en.

Edit: Termistön osalta tämä kirjoitus on helppo tapa päästä alkuvauhtiin: 400 Trading Algorithms Later

 

[Manual]

Harrastin ensimmäistä kertaa ikinä loppuvuoden alle 1000e myyntiä, mutta havaitsin nyt että tuo kauppa taisi mennä osittain tämän vuoden puolelle…? Menikö tämä veroetu nyt mönkään ja tämän vuoden rajaan vai ei?

 

[xylitoli]

Harrastin ensimmäistä kertaa ikinä loppuvuoden alle 1000e myyntiä, mutta havaitsin nyt että tuo kauppa taisi mennä osittain tämän vuoden puolelle…? Menikö tämä veroetu nyt mönkään ja tämän vuoden rajaan vai ei?

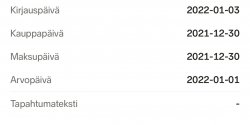
Kun kauppapäivä on viime vuonna, niin se ratkaisee. Muut rivit kuvassa eivät tietääkseni ole Suomen verotukseen vaikuttavia.

 

[Nomber]

Jep, tässä on maailma ajettu siihen tilanteeseen että kumpikin vaihtoehdoista on todella huono. Joko annettava inflaation laukata vapaasti ja talous kaatuu siihen tai sitten nostettava korkoja reilusti ja talous kaatuu siihen. Oikeastaan kysymys ei enää ole että kaatuuko talous vaan että kuinka pahasti.

Tosin onko oikein mitään hyvää vaihtoehtoa? Jos lainaa ei olisi niin ei olisi oikein mitään muutakaan? Firmat ja valtiot pyörivät lainarahalla ja ihmisille on tarjolla kaikkea ja paljon. Jos kukaan ei ottaisi lainaa niin aika vähän olisi tarjolla mitään. Toki sitten aina välillä tulee väistämätön romahdus kun lainaa on liikaa. Koko tekninen kehitys ja hyvin vointi perustuu vain lainaan lopulta kuitenkin. En tiedä miten tämän voisi muutenkaan hoitaa? Ja toisaalta jos aina saa 20 vuotta elää hyvää nousukautta ja sitten jonkunaikaa lamaa niin onko se lopulta niin huono jos vertaa siihen, että koskaan ei ole oikein mitään? No riippuu toki keneltä kysyy.

 

[tuoppi´]

Tosin onko oikein mitään hyvää vaihtoehtoa? Jos lainaa ei olisi niin ei olisi oikein mitään muutakaan? Firmat ja valtiot pyörivät lainarahalla ja ihmisille on tarjolla kaikkea ja paljon. Jos kukaan ei ottaisi lainaa niin aika vähän olisi tarjolla mitään. Toki sitten aina välillä tulee väistämätön romahdus kun lainaa on liikaa. Koko tekninen kehitys ja hyvin vointi perustuu vain lainaan lopulta kuitenkin. En tiedä miten tämän voisi muutenkaan hoitaa? Ja toisaalta jos aina saa 20 vuotta elää hyvää nousukautta ja sitten jonkunaikaa lamaa niin onko se lopulta niin huono jos vertaa siihen, että koskaan ei ole oikein mitään? No riippuu toki keneltä kysyy.

Ei laina itsessään olekkaan paha ja kuten sanoit siihen perustuu iso osa hyvinvoinnista ja kehityksestä. Mutta pitää muistaa että, se laina pitää aina maksaa takaisin, jos ei korkojen muodossa niin sitten inflaationa.

Romahdusten funktio on juuri se, että ne nollaa tilannetta. Mutta nyt sitä romahdusta ollaan aina vaan lykätty ja lykätty niin se nollattavan määrä on siellä taustalla vaan kasvanut. Jossain vaiheessa sitä ei voi enää lykätä ja mitä isommaksi se on kasvanut niin sitä pahempi se nollaus tulee olemaan. Sitä ei voi kukaan sanoa varmasti miltä se tulee sitten näyttämään, mutta eiköhän se ole vähän pahempi kuin "jonkunaikaa lamaa".

 

[zepi]

Jep, tässä on maailma ajettu siihen tilanteeseen että kumpikin vaihtoehdoista on todella huono. Joko annettava inflaation laukata vapaasti ja talous kaatuu siihen tai sitten nostettava korkoja reilusti ja talous kaatuu siihen. Oikeastaan kysymys ei enää ole että kaatuuko talous vaan että kuinka pahasti.

En kyllä näe, että nämä olisivat ainoat tarjolla olevat vaihtoehdot. Korkojen vatvomisen sijaan vois markkinoilta kerätä likvidiä pois esim. Pienentämällä keskuspankkien taseita (myymällä omistuksia), ja silloin kun kierrossa olevan rahan määrä vähenee, inflaatio kyllä hidastuu.

5Y bondin tips spread jenkeissä ei ennakoi mitään katastrofaalista inflaatiota - joskin se on nyt n. 2.8-2.9%.

5 Year TIPS/Treasury Breakeven Rate Market Daily Trends: H.15 Selected Interest Rates | YCharts

In depth view into 5 Year TIPS/Treasury Breakeven Rate including historical data from 2003 to 2024, charts and stats.

ycharts.com

 

[tuoppi´]

En kyllä näe, että nämä olisivat ainoat tarjolla olevat vaihtoehdot. Korkojen vatvomisen sijaan vois markkinoilta kerätä likvidiä pois esim. Pienentämällä keskuspankkien taseita (myymällä omistuksia), ja silloin kun kierrossa olevan rahan määrä vähenee, inflaatio kyllä hidastuu.

5Y bondin tips spread jenkeissä ei ennakoi mitään katastrofaalista inflaatiota - joskin se on nyt n. 2.8-2.9%.

5 Year TIPS/Treasury Breakeven Rate Market Daily Trends: H.15 Selected Interest Rates | YCharts

In depth view into 5 Year TIPS/Treasury Breakeven Rate including historical data from 2003 to 2024, charts and stats.

ycharts.com

Noilla vaihtoehtoisilla tavoillakin on käytännössä sama vaikutus kuin korkojen nostolla. QE:tä ei voi lopettaa lopettamatta QE:ta.

Ennakoinnista en tiiä, mutta jenkeissähän on inflaatio suurempi kuin 40 vuoteen jo (7%). Ja tuo CPI:llä mitattuna, mistä on otettu pois niitä osia missä inflaatio eniten näkyy. "Todellinen" inflaatio on luultavasti vielä tuotakin suurempi.

 

[zepi]

Noilla vaihtoehtoisilla tavoillakin on käytännössä sama vaikutus kuin korkojen nostolla. QE:tä ei voi lopettaa lopettamatta QE:ta.

Ennakoinnista en tiiä, mutta jenkeissähän on inflaatio suurempi kuin 40 vuoteen jo (7%). Ja tuo CPI:llä mitattuna, mistä on otettu pois niitä osia missä inflaatio eniten näkyy. "Todellinen" inflaatio on luultavasti vielä tuotakin suurempi.

QE:n lopettaminen, hidastaminen, säätäminen jne. ovat kuitenkin tarjolla olevia keinoja. Pelkät ohjauskoron nostot ja laskut eivät ole ainoa keino vaikuttaa rahapolitiikkaan.

Se, että mitä niistä käytetään on sitten eri asia. Jenkeissä muistetaan vielä se, kuinka FED on aiheuttanut monta lamaa nostelemalla korkoja harkitsemattomasti.

 

[Pöllömies]

Yritysten liiketoimintojen ja tulosten reaalinen kasvu sen lopulta määrittää, miten tässä käy. Monet yritykset ovat kyllä vakavaraisia ja velkarahoitus hallinnassa, mutta kasvu on monilla pysähtynyt. Se on jossain määrin huolestuttavaa. Ilman kasvua on vaikea nähdä markkinoiden vakauden ainakaan paranevan pitkällä aikavälillä. Liikkeellä olevan rahan määrä kasvaa ja samaaan aikaan piensijoittajien määrä kasvaa. Toisin sanoen yhä useampi sijoittaja ja suurempi raha kilpailee samoista tuotoista. Tämä on kestävää sijoittajien kannalta ainoastaan yritysten tulosten kasvaessa.

Ruohonjuuritasolla näkyy yritysjohtajien liian varovainen investointistrategia, mikä on ollut jo ainakin 20 vuotta enemmän tai vähemmän tyypillistä varsinkin Suomi-yrityksille. Tulevaisuuden kasvu on aivan keskeisen riippuvainen yritysten investoinneista. Jos kuluneen 20 vuoden aikana markkinoiden arvostuksen kasvu on pitkälti perustunut elvytykseen, niin on sanomattakin selvää että elvytysmekanismin rikkoutuessa ainoa tie ulos mahdollisimman kuivin jaloin on yritysten reaalinen kyky tehdä sitä todellista kasvua.

 

[tuoppi´]

QE:n lopettaminen, hidastaminen, säätäminen jne. ovat kuitenkin tarjolla olevia keinoja. Pelkät ohjauskoron nostot ja laskut eivät ole ainoa keino vaikuttaa rahapolitiikkaan.

Se, että mitä niistä käytetään on sitten eri asia. Jenkeissä muistetaan vielä se, kuinka FED on aiheuttanut monta lamaa nostelemalla korkoja harkitsemattomasti.

Joo, onhan noita toki muitakin tapoja. Mutta ei ne muutkaan tavat ole sen parempia lopputulokseltaan. Tilanne on sellainen että sitä lamaa ei voi oikein estää millään. Korjausliikkeet ovat joko liian isoja tai liian pieniä, sellaista "sopivaa" tasoa ei enää ole.

 

[zepi]

Joo, onhan noita toki muitakin tapoja. Mutta ei ne muutkaan tavat ole sen parempia lopputulokseltaan. Tilanne on sellainen että sitä lamaa ei voi oikein estää millään. Korjausliikkeet ovat joko liian isoja tai liian pieniä, sellaista "sopivaa" tasoa ei enää ole.

Yleensä kun systeemi uhkaa karata epätasapainoon / olla epästabiili, siihen lisätään negatiivista takaisinkytkentää joka tasapainottaa systeemin.

Sitä odotellessa, että ensimmäinen keskuspankki lopettaa käsin räveltämisen ja alkaa määrittää algoritmisesti ohjauskoron ja QE:n määrän takaisinkytkemällä esim. työllisyys, inflaatio ja ngdp-lukemia tai vielä parempaa - niiden johdannaisia.

En kyllä pidätä hengitystä, että maailma olisi valmis.

 

[dropadrop]

Jos jokainen kriisi on erilainen tarvitaan sen ratkaisemiseksi eri toimenpiteitä. Se varmaan vaikeuttaa tommosen maagisen algoritmin tekemistä.

Keskuspankit ovat varmaan nytkin ihan hyviä estämään pari edellistä kriisiä, siinä tohinassa vaan helposti luovat uuden.

 

[tuoppi´]

Itse olen sillä kannalla, että mitä vähemmän markkinoita yritetään manipuloida niin sitä parempi. Markkinat ja talous ovat kuitenkin itseään korjaavia systeemejä ja enemmän siitä vaan tulee ongelmia kun yritetään taistella vastaan. Ehkä romahduksia ja korjausliikkeitä tulisi useammin, mutta ne olisivat pienempiä ja kokonaisuutena talous olisi kestävämmällä pohjalla.

 

[Pöllömies]

Hieman turhauttava tämä markkinatilanne kyllä, kun himoitsemani osakkeet ylittävät edelleen tavoiteostohintani selvästi samalla kun käyrät ovat jo kolmatta kuukautta kulkeneet vaakatasossa. Eli tuottoa ei ole marraskuun jälkeen hirveästi omistuksille syntynyt samalla kun mitään uutta ei oikein pysty myöskään ostamaankaan. Saa nähdä kauanko tällainen tilanne nyt jatkuu sitten.

 

[kmot]

Eiköhän osakemarkkinoilla nähdä kohta lisää volatiliteettia, jos/kun Venäjä aloittaa operaationsa Ukrainassa.

 

[Nomber]

Eiköhän osakemarkkinoilla nähdä kohta lisää volatiliteettia, jos/kun Venäjä aloittaa operaationsa Ukrainassa.

Onneksi on hyvin hajautettu itselläni maailmalle, voi olla että tulee helsingin pörssi rytinällä alas jos putin aloittaa operaation suomessa. Eipä voi noista venäläisistä kyllä yhtään tietää mitä aikovat.

 

[Lämpöpumppu]

Onneksi on hyvin hajautettu itselläni maailmalle, voi olla että tulee helsingin pörssi rytinällä alas jos putin aloittaa operaation suomessa. Eipä voi noista venäläisistä kyllä yhtään tietää mitä aikovat.

Eiköhän Venäjän toimilla ole vaikutuksia ihan globaalillakin tasolla ainakin länsimaiden markkinoilla, kun vaikutukset näkyvät Euroopassa ja Pohjois-Amerikassa. Kehittyvät Aasian markkinat voivat olla turvallisemmassa asemassa.

 

[Mastah]

Eiköhän Venäjän toimilla ole vaikutuksia ihan globaalillakin tasolla ainakin länsimaiden markkinoilla, kun vaikutukset näkyvät Euroopassa ja Pohjois-Amerikassa. Kehittyvät Aasian markkinat voivat olla turvallisemmassa asemassa.

Sotia on ollut ennenkin ja niillä on ollut yllättävän pieni vaikutus pörsseihin, ja kurssit on tainneet jopa keskimäärin nousta silloin. Sen päälle Venäjän osuus on alle 2%:ia koko maailman BKT:stä ja nykyään monilta osin aika eristäytynyt kaikenlaisesta talousyhteistyöstä. Tuokin vähäinen BKT tulee paljolti raaka-aineista, eikä Venäjällä ole oikein varaa lopettaa niiden vientiä. Pitäisin tuota aika pienenä osatekijänä moniin muihin tämän hetken riskeihin verrattuna.

 

[Lämpöpumppu]

Sotia on ollut ennenkin ja niillä on ollut yllättävän pieni vaikutus pörsseihin, ja kurssit on tainneet jopa keskimäärin nousta silloin. Sen päälle Venäjän osuus on alle 2%:ia koko maailman BKT:stä ja nykyään monilta osin aika eristäytynyt kaikenlaisesta talousyhteistyöstä. Pitäisin tuota aika pienenä osatekijänä moniin muihin tämän hetken riskeihin verrattuna.

Toisaalta markkinoilla on sen verran paljon ilmaa ja paljon hypeä, mikä saattaisi sodan alkaessa laukaista isommankin pudotuksen.

 

[zepi]

Toisaalta markkinoilla on sen verran paljon ilmaa ja paljon hypeä, mikä saattaisi sodan alkaessa laukaista isommankin pudotuksen.

Keskuspankeilla on edelleen jalka tukevasti setelipainon kaasulla, joten vaikea on kyllä ennustaa kovin suurta tiputusta kunhan Putin malttaa pitää ydinaseet tiukasti jemmassa.

 

[ANTI_L]

Keskuspankeilla on edelleen jalka tukevasti setelipainon kaasulla, joten vaikea on kyllä ennustaa kovin suurta tiputusta kunhan Putin malttaa pitää ydinaseet tiukasti jemmassa.

Menee kyllä pahasti politiikan puolelle, mutta onhan se Putin aika huomionkipeä kakara, kun ei hoida oman maan asioita kuntoon vaan uhittelee vain muille.

Mitä näihin sijoitushommiin tulee, niin ehkä tässä maailmantilanteessa kannattaa hajaannuttaa sijoitukset ympäri maailmaa niin, että pieni sota siellä sun täällä ei vaikuta paljon sijoituksiin.

 

[xylitoli]

Pörssireaktio riippuu myös paljon siitä minkä muotoinen ja kuinka pitkä sota tulisi. Siis vaihtoehdoista pelkkää uhittelua / kyberiä ja paikallisten aseistamista / vähäisiä piilo-operaatioita / täysimittainen Rus vs Ukr maa- & ilmasota (salamasota/asemasota) / Rus tekisi operaatioita muuallakin kuin Ukr / Nato tulisi mukaan / Kiina hyödyntäisi tilannetta omalla suunnallaan / Kiina & Rus liittoutuisivat / joku (kuten n.Kr.) räjäyttäisi nuken avaruudessa / täysimittainen WWIII ilman nukeja tai niiden kanssa jne.

Aika selvä ettei äkkiseltään ajateltuna kenenkään järkevissä intresseissä ole sotia kuin korkeintaan näytösluontoisesti Ukrainan tasangoilla.
Mutta entä jos Putinilla on korviensa välissä joku vimma päästä historian kirjoihin riippumatta uhrien määrästä?

Niin tai näin, niin tässä kohtaa ei voi vielä rehellisyyden nimissä sulkea pois pahinpiakaan skenaarioita, vaikka todennäköisintä onkin että Putin lähinnä kokeilee saako puhumalla (venäjällä heikkona pidetyn) Bidenin laskemaan allensa.

 

[fatrick]

Herännyt kiinostus QT groupista kurssilaskun myötä. Lyhyellä aikavälillä kurssi voi vielä lasketella rajustikin yleisen sekavuuden vallitessa maailman markkinoilla. On sirupulaa, Venäjä pullistelee, Inflaatio jne. Mutta pitkällä aikavälillä tässä on ainekset mihin vain +5 vuotta. Kaupallinen puoli on viimeisten parin vuoden aikana näyttänyt toimivan. Onko tekkiläiset kuinka perillä QT:n frameworkistä? Lähinnä kiinostaa kilpailutilanne ja voisiko tuollaisen frameworkin värkätä kuinka helposti itse? Asiakkaina ovat kuitenkin aivan eri kokoluokan softatalot, joilla on varmasti osaamista/muskeleita tehdä oma jos niin haluavat. Youtubesta löytyy vielä kovin vähän QT ulkopuolisten devaajien tutoriaaleja, joka on mielestäni huono juttu.

 

[dropadrop]

Meillä syyteltiin aina QT’ta kun valittelin käyttöliittymien ärsyttäviä bugeja… Nyt pidemmän aikaa kaikki tuotteen ovat siirtyneet QT’sta pois, ja devaajat ovat olleet tosi tyytyväisiä.

Ongelma voi toki olla firman sisäisissä toimintamalleissa, tai ajatuksessa käyttää samaa frameworkkiä kaikkialla. Tällä suppealla kokemuksella olen kuitenkin pysynyt osakkeesta erossa.

 

[kuoris]

Meillä syyteltiin aina QT’ta kun valittelin käyttöliittymien ärsyttäviä bugeja… Nyt pidemmän aikaa kaikki tuotteen ovat siirtyneet QT’sta pois, ja devaajat ovat olleet tosi tyytyväisiä.

QT:tä en itse ole käyttänyt sulautetuissa projekteissa mutta mitä kollegoilta kuullut niin se on turhan kallis moneen projektiin. Jonkun kurssin siitä kävin yli 10 vuotta sitten mutta varmaan muuttunut sen jälkeen. Osake on mielestäni yliarvostettu.

 

[dropadrop]

Kallis on välillä hankala määritellä. Meillä on ollut käytössä yksi devaajia tukeva järjestelmä joka maksaa suunilleen saman kuin 1 devaaja. Mä näkisin, että se säästää 2 devaajan tarpeen, eli on kannattava (mut joka vuosi kun lasku tulee keskustellaan siitä, miten voi olla noin vitun kallis).

QT kai myytiin meille (ennen mun aikoja) ajatuksella, että helppo tehdä eri käyttiksille samannäköinen käyttöliittymä. Mun mielestä jo lähtökohtaisesti se saattaa olla tyhmä idea jolleivat käyttäjät usein siirry alustojen välillä. Meillä eri alustojen devaajat vaikuttavat olevan oman alustansa experttejä, ja heille oman alustan natiivit kirjastot tuntuvat oikeilta.

 

[Harb]

Huomasin että OP ryhmän tuotto-osuuksien tuottotavoite on 4,45% vuodelle 2022.

Olen aikaisemmin harrastanut Tradekan tuotto-osuuksia joiden korko on EDIT: 3,5% (kiitos @Kvarkki ) mutta OP:n riski on tietysti pienempi.

Tämänhetkisessä markkinatilanteessa alkoi taas kiinnostamaan kun lyhyen aikavälin markkinat ovat aika volatiileja ja keskipitkällä aikavälillä on negatiivista potentiaalia.

Ongelmahan noissa on pitkähkö sijoitusaika (voi lunastaa merkintää seuraavan vuoden lopussa) ja se että niille ei ole talletussuojaa mutta jos on valmis tuon riskin hyväksymään niin 4,5% on ihan kohtuullinen tuotto varsinkin kun huomioi lievän verokohtelun. Tosin OP:n osalta tuo 4,45% on todennäköisesti ainoastaan hetkellinen.

 

[Kvarkki]

Tradekan tavoite on kyllä 3,5% Pääomasuojaamattomana en varsinkaan tradekan osuuksia kyllä ostais, toveri varmasti keksii keinon jos toisen varastaa muiden rahat vuosien mittaan.

 

[zepi]

Tuottotavoite on kyllä hauska termi. Voihan sitä tavoitteena olla vaikka +50%. Se on sitten ihan eri asia, että mihin pystytään...

 

[vermont]

Tuottotavoite on kyllä hauska termi. Voihan sitä tavoitteena olla vaikka +50%. Se on sitten ihan eri asia, että mihin pystytään...

Johan CAP-mallista lähtien puhutaan tuotto-odotuksista/-tavoitteista. Prosyyrissä kyseiset tuotto-odotukset kun vain pyrkivät helpottamaan tarjottavien tuotteiden välistä vertailua, ehkä selkeämpi olisi kuvata esim. osake-/korko-osuuksien suhdetta + kyseisten osuuksien riskisyyttä (beta jne).

 

[PornReindeer]

Mites vaikka 50k€ lyhyellä tähtäimellä?

Minulla on nyt rahaa tilillä, mutta ne (ainakin iso osa) tullaan laittamaan asuntoon remppoihin. Tarkoitus ei kuitenkaan ole tuoda puskutraktoria paikalle vaan isoista rempoista ehkä kesällä pikkuvessa/suihku, keittiö mahdollisesti vuoden päästä ja siitä joskus tulevaisuudessa khh+kylppäri+sauna.

Rahaa tulee toki palkan muodossa joka kuussa ja hyvä kysymys onkon paljonko remppoihin tullaan oikeasti laittamaan rahaa. Tilillä makuuttaminen pari vuotta ja sitten parin vuoden päästä ylijääneen saldon sijoittaminen siinä vaiheessa ei kuulosta järkevältä. Toisaalta jos alkaisi vaan pikkusummalla (muutaman vuoden edit. ajallisella hajauttamisella 1000-2000€ /kk) siirtämään rahoja vaikka johonkin rahastoon ja maksaisi ekat rempat tililtä, sitten kun näyttää että tilin rahat ei riitä niin nostaisi tarpeen mukaan

 

[Carmake]

Toisaalta jos alkaisi vaan pikkusummalla (muutaman vuoden kokonaisajalla) siirtämään rahoja vaikka johonkin rahastoon ja maksaisi ekat rempat tililtä, sitten kun näyttää että tilin rahat ei riitä niin nostaisi tarpeen mukaan

Muutama vuosi on sijoittamisessa varsin lyhyt aika. Yleisesti sanoisin, että älä sijoita rahaa, mitä saatat tarvita hetken päästä. Voit joutua nostamaan rahaa sijoitustililtä juuri silloin, kun kurssit ovat pahasti laskussa ja tätähän me emme halua tehdä.