Zigh
Tittelitön
- Liittynyt
- 17.10.2016
- Viestejä
- 5 119
Edit: ei kun ei tämäkään välttämättä toimi kaikissa tapauksissa
Pieniä kysymyksiä ohjelmoinnista
- Keskustelun aloittaja Kautium
- Aloitettu
-
- Avainsanat
- kysymys ohjelmointi pulma
Edit: ei kun ei tämäkään välttämättä toimi kaikissa tapauksissa
- Liittynyt
- 29.10.2016
- Viestejä
- 4 431
Ei ehkä tehokkain tapa, mutta voisit lähteä liikkeelle siitä, että purat kolmiot kolmeen vektoriin. Vektorin etäisyyden pisteeseen voit laskea esim näillä ohjeilla: Shortest distance between a point and a line segment
Vektorit sitten jotenkin liität siihen kolmiotietoon. En ainakaan äkkiseltään keksi mitään suoraa ratkaisua, jos puhutaan puhtaasti yksinkertaisesta ohjelmoinnista. Toki jos kyseessä on joku pelikehitys tmv. niin varmasti valmiita kirjastoja tuollaisen laskentaan.
Vektorit sitten jotenkin liität siihen kolmiotietoon. En ainakaan äkkiseltään keksi mitään suoraa ratkaisua, jos puhutaan puhtaasti yksinkertaisesta ohjelmoinnista. Toki jos kyseessä on joku pelikehitys tmv. niin varmasti valmiita kirjastoja tuollaisen laskentaan.
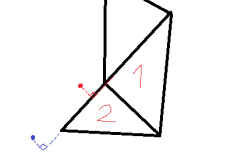
Äkkiä miettien ainakaan varsinaista etäisyyttä ei tarvitse laskea. Etäisyyden voi laskea Pythagoraan kaavalla, jos vain pystyy määrittelemään kolmiosta sen pisteen joka on lähimpänä pistettä. Etäisyys siis vaatisi vielä neliöjuurta, mutta sen laskeminen on turhaa.
Lähimmän pisteen saisi kyllä laskettua ainakin niin, että piirrät kolmion keskipisteestä suoran viivan pisteeseen. Lähin kohta on se, missä tämä viiva leikkaa kolmion reunan. Se näistä kohdista, mikä on lähimpänä on lähin kolmio.
Ei kylläkään kovin tehokas tapa, joten voi olla että tähän on parempikin algoritmi.
Lähimmän pisteen saisi kyllä laskettua ainakin niin, että piirrät kolmion keskipisteestä suoran viivan pisteeseen. Lähin kohta on se, missä tämä viiva leikkaa kolmion reunan. Se näistä kohdista, mikä on lähimpänä on lähin kolmio.
Ei kylläkään kovin tehokas tapa, joten voi olla että tähän on parempikin algoritmi.
Ei kyllä voi toimia niin että lasketaan kolmion keskipisteestä etäisyyttä ja valitaan se jolla on lyhin etäisyys. Esim toisessa kolmiossa sivun mitta voi olla vaikka 1000 ja toisessa 10. Kuitenkin 1000 mittainen kolmio voi olla lähempänä.
Tätä minäkin ajattelin, mutta ongelmana taitaa olla tämmöinen, valitaanko kolmio 1 vai 2. Pisteet punaisella ja sinisellä.
Liitteet
Zigh
Tittelitön
- Liittynyt
- 17.10.2016
- Viestejä
- 5 119
Mikä tuossa on ongelma? Kyllä tuon etäisyys suoralle -ratkaisun pitäisi toimia. Neliöjuuria ei tosiaan kannata laskea kuin vasta jos on ihan pakko.Tätä minäkin ajattelin, mutta ongelmana taitaa olla tämmöinen, valitaanko kolmio 1 vai 2. Pisteet punaisella ja sinisellä.
- Liittynyt
- 29.10.2016
- Viestejä
- 4 431
Eikö tuossa ole silloin ihan sama kumpi valitaan tai valitaan molemmat, jos etäisyys on tismalleen sama?
Ei. Koska toinen kolmio on lähempänä, kuten kuvasta näkyy. Suorakulmainen etäisyys on kuitenkin sama.
Zigh
Tittelitön
- Liittynyt
- 17.10.2016
- Viestejä
- 5 119
No joku lisäkriteeri sitten jos niille pitää joku ero saada. Esim. etäisyys kaikkiin kolmion kulmiin yhteensä -> pienempi "lähempänä".
Mutta tätä ei ollut alkuperäisessä kysymyksessä.
Zigh
Tittelitön
- Liittynyt
- 17.10.2016
- Viestejä
- 5 119
Jos lyhin etäisyys on sama, niin eihän se toinen silloin ole lähempänä
Ehkä joo tämä voisi toimia. Ei ollut alkuperäisessä kysymyksessä toki, kun tätä tässä samalla yritän pohtia..
Eikö tuosta näe että sininen piste on lähempänä 2 kolmiota, vaikka etäisyys on sekä 1 että 2 kolmioon sama.Jos lyhin etäisyys on sama, niin eihän se toinen silloin ole lähempänä
tässä taitaa tulla ongelmaksi tämä, eli jos tuon kakkoskolmion terävä kärki karkaa todella kauas, jolloin kärkien yhteenlaskettua etäisyyttä laskemalla saadaan lähimmäksi kolmioksi ykkönen.:
Zigh
Tittelitön
- Liittynyt
- 17.10.2016
- Viestejä
- 5 119
Siis onko kolmio 2 kolmion 1 sisällä?
Toisaalta ei tämäkään muuta asiaa mihinkään jos vain haetaan mitä tahansa kolmion pistettä joka on lähinnä.
Jos taas haetaan esim. kolmion massakeskipistettä, niin sitten pitää laskea sillä.
Ei ole kolmiot toistensa sisällä
- Liittynyt
- 29.10.2016
- Viestejä
- 4 431
Nyt en kyllä enää ymmärrä mitä tässä yritetään laskea?tässä taitaa tulla ongelmaksi tämä, eli jos tuon kakkoskolmion terävä kärki karkaa todella kauas, jolloin kärkien yhteenlaskettua etäisyyttä laskemalla saadaan lähimmäksi kolmioksi ykkönen.:
Alkuperäsisessä kuvauksessa annoit ymmärtää, että haetaan raa'asti lähintä kolmiota, eli mitataan etäisyys kolmion lähimpään sivuun/kulmaan ja valitaan se kolmio. nyt tässä taas mietitään kärkivälejä? Eikö tämä jälkimäinen skenaario nyt ratkea sillä, että lasket kolmioiden keskipisteen ja siitä mittaat etäisyyden sitten pisteisiin x,y,z?
emagdnim
Tukijäsen
- Liittynyt
- 21.10.2016
- Viestejä
- 11 989
Valitaan vain kaks lähintä kulmaa jokaiselta kolmiolta?tässä taitaa tulla ongelmaksi tämä, eli jos tuon kakkoskolmion terävä kärki karkaa todella kauas, jolloin kärkien yhteenlaskettua etäisyyttä laskemalla saadaan lähimmäksi kolmioksi ykkönen.:
Zigh
Tittelitön
- Liittynyt
- 17.10.2016
- Viestejä
- 5 119
Eikö tässä kakkosen lähin piste ole huomattavasti lähempänä kuin ykkösen jolloin muuta ei enää tarvita?tässä taitaa tulla ongelmaksi tämä, eli jos tuon kakkoskolmion terävä kärki karkaa todella kauas, jolloin kärkien yhteenlaskettua etäisyyttä laskemalla saadaan lähimmäksi kolmioksi ykkönen.:
Ihan sama tuossa aiemmassa kuvassa siniselle pisteelle.
Kolmion keskipisteestä ei tosiaan tarvitse laskea etäisyyttä, tarkoitin että se vertailtava piste on se kohta, jossa kolmion keskipisteestä lähtevä viiva leikkaa kolmion sivun. Tuo piste on kolmion lähin kohta.
Edelleen haetaan raa'asti lähintä kolmiota. Kumpi kolmion keskipiste on lähempänä sinistä pistettä? Ykköskolmion keskipiste voi olla lähmpänä, varsinkin jos tuo kakkoskolmion kärki karkaa todella kauas. Kuitenkin kakkoskolmio on sinistä pistettä lähempänä.Nyt en kyllä enää ymmärrä mitä tässä yritetään laskea?
Zigh
Tittelitön
- Liittynyt
- 17.10.2016
- Viestejä
- 5 119
Ei mene näin. Tällä tavalla et saa lähintä pistettä.
Zigh
Tittelitön
- Liittynyt
- 17.10.2016
- Viestejä
- 5 119
Sun pitää määritellä mikä on lähin kolmio. Onko se lähimmän pisteen mukaan, kolmion massakeskipisteen mukaan vai esim. kulmien keskimääräisen etäisyyden mukaan?
Ehkä joo näin toimii. Täytyy koittaa.
Minimietäisyys kolmion reunoihin nähden.
Varmaan 2- osaisella päättelyllä kun kaikki yllä olevat ehdotukset yhdistetään:
1. jonkin kolmion kärkipiste on lähempänä kuin mikään muu kärki -> valitaan ko kolmio
2. jos kahdella tai useammalla kolmiolla osuu kärki yhtä lähelle niin silloin tutkitaan näistä kolmioista muutkin kulma -> valitaan lähin.
jos edelleen sama tulos pitää valita jollakin perusteella (koordinaatistossa ylempänä/alempana/oikealla/vasemmalla, järjestyksessä ensimmäinen/viimeinen, jne) kumpi/mikä on lähin kolmio.
Sitten on tämä tilanne johon tuo yllä oleva ei ehkä sovellu jos halutaan kolmion X olevan lähin Y:n sijaan.
- Liittynyt
- 19.10.2016
- Viestejä
- 3 778
Kärkipisteen perusteella voi löytyä väärä.
Liitteet
emagdnim
Tukijäsen
- Liittynyt
- 21.10.2016
- Viestejä
- 11 989
1. etsitään lähimmät kulmat,
2. jos on yhtä lähellä useampi, nii sit valitaan toiseksi lähimmät kulmat lisäksi näiltä yhtä lähellä olevista. Näiden kahden kulman keskikohtaan sit vertailu?
edit: eiku ei sekää toimis tossa esimerkissä
vois eka lukea uusimmat viestit ennenku vastaa...Nope. ojisaman esimerkissä lähin olisi tuo pienempi ja kauempi kolmio.
e2: uus yritys. etsitään siis lähintä kolmion sivua. En kyl nyt osaa pikaisesti mitää järkevää algoritmia miettiä, mut eikös se ole kolmioiden kahden lähimmän kulman keskikohdasta pisteesteen, johon etäisyyttä lasketaan?
eli esim. tossa ojisaman esimerkissä näin:
e3: ei toimi tuokaan (siirrä piste ylemmän kolmion vasempaan nurkkaan). Luovutan. Vaatinee jotain parempaa matematiikkaa tai iffittelyä.
e4: entäpä noiden yhdistelmä? Lähin kulma + lähin 2 kahden kulman keskikohta ja niistä sit kolmiogeometriaa eli näiden keskikohdasta pisteeseen?
en siis vektoreiden päälle ymmärrä, jos joku mun ajattelutapaa ihmettelee.eli tähän tyyliin, jos kuvasta tolkkua saa:
Kolmion keskikohdasta lähin leikkaus pisteeseen ei toimi, koska esim. toi ylempi kolmio voisi jatkua ties kuinka pitkälle, joka tarkoittaa, että tämä minunkaan ajatus ei edelleenkään toimi.
Viimeksi muokattu:
- Liittynyt
- 19.10.2016
- Viestejä
- 3 778
Tuossa tapauksessa voidaan tarkistaa osuuko tuo minimietäisyys oikeasti johonkin kolmioon. Näpppituntumalta se kulma niistä kolmioista joihin tuo mätsää on se lähin, jos niitä sivuja on samalla suoralla.
Totta.
Varmaan pitää lisätä tarkastukseen suoran ja pisteen välinen etäisyys. Ja pienempi voittaa.
Joka tapauksessa ei taida olla olemassa yhtä tapaa joka vastaa kysymykseen
- Liittynyt
- 18.10.2016
- Viestejä
- 111
Jos haluat puhtaasti matemaattista ratkasua niin kantsii kysellä matikkathreadissa: Matikkatriidi - apuja matemaattisiin pulmiin Menee OT:n puolelle kun ei olekkaan ohjelmointikysymys mutta OP vissiin etsii tätä: Barysentrinen koordinaatti (geometria) – Wikipedia ja valmis ratkasu kolmessa ulottuvuudessa: Minimum distance between point and face
Ehkäpä @hissukka voinee avata mikä on kupletin juoni tässä?
En usko että nyt tarvitsee käyttää mitään ratkaisua kolmessa ulottuvuudessa, koska kyseessä on puhtaasti 2d pulma. Face on kolmiuloitteinen kappale, jossa esimerkiksi jokaisella nurkkapisteellä on eri Z arvo. Eikö tuo ratkaisu mahda antaa minimietäisyyden siihen faceen, sen Z etäisyyden.
Pulma liittyy tekemääni softaan, joka extrapoloi korkeutta kolmiulotteisesta kolmioverkosta, kunhan ensin oikea face(kolmio) löytyy.
Pisteen etäisyyden laskenta kolmion lähimpään reunaan riippuu siitä onko piste kohtisuorassa kolmion johonkin sivuun nähden (1.) vai ei (2.). Kuvassa on jaoteltu nuo alueet pitkällä katkoviivalla ja lyhyellä katkoviivalla on hahmoteltu pisteitä, jotka ovat kaikki samalla etäisyydellä kolmiosta. Tapauksessa 1. etäisyys lasketaan suoran ja pisteen etäisyytenä, minkä laskemiseen taisikin jossain aiemmassa viestissä olla linkki. Tapauksessa 2. taas etäisyys on kolmion nurkan ja pisteen välinen etäisyys.
- Liittynyt
- 19.12.2016
- Viestejä
- 234
Ei ollu ihan pieni kysymys ohjelmoinnista
Ei kovin ihmeellinenkään. Aika perus. Tuolla yllä se vastaus jo on ja @ade07 sen tuossa vielä graafisestikin esittää.
- Liittynyt
- 19.10.2016
- Viestejä
- 3 778
Joskaan tuo esitys ei kerro miten se vertailu tapahtuu.
Mutta kyllä joo, sen kolmiulotteisen laskennan erikoistapaukset osuu tähän.
Ihan mielenkiinnosta, niin mitä tässä oletettiin tiedetyksi muuta kuin tutkittavan pisteen koordinaatit? Tuo etäisyyden laskeminen matemaattisesti ihan selvää, mutta lähinnä en tajunnut, mitä iloa tuosta matikasta yksinään on, jos et tiedä yhtään, missä päin tasoa kolmiot on ja miten päin.
Kursin kasaan yksinkertaisen python esimerkin tuolla stackowerflown koodilla. Tuo dist() funktio oli tehty ottamaan huomioon nuo nurkat suoraan (tuo u rajoitus 0 ja 1 välille), joten niitä ei tarvitse erikseen tutkia.
Python:
# Mukailtu https://stackoverflow.com/a/2233538
def dist(p1, p2, p):
px = p2[0] - p1[0]
py = p2[1] - p1[1]
norm = px * px + py * py
u = ((p[0] - p1[0]) * px + (p[1] - p1[1]) * py) / norm
if u > 1:
u = 1
elif u < 0:
u = 0
x = p1[0] + u * px
y = p1[1] + u * py
dx = x - p[0]
dy = y - p[1]
return (dx * dx + dy * dy) ** 0.5
def kolmion_etäisyys(piste, kolmio):
return min(dist(kolmio[0], kolmio[1], piste),
dist(kolmio[1], kolmio[2], piste),
dist(kolmio[2], kolmio[0], piste))
kolmio = ((2,1), (6,2), (4,3))
piste1 = (2,3)
piste2 = (4,3.5)
print(kolmion_etäisyys(piste1, kolmio))
print(kolmion_etäisyys(piste2, kolmio))Vastaukseksi tuosta tulee järkevät:
$ python kolmio.py
1.4142135623730951
0.5Tilanteesta plotti näyttää tältä:
Yksinkertaisin tapa muuttaa tuo toimimaan usealla kolmiolla on loopata kaikki kolmiot läpi tuolla samalla tavalla ja valita niistä sitten lähin. Jos kolmioita on valtavan paljon ne kannattaisi etukäteen järjestellä pienempiin alueisiin jolloin voidaan tutkia vain se alue, jossa piste on ja mahdollisesti viereiset. Aluejaon tekeminen on sitten tietty aivan oma hommansa. Tuollaista jakoa käsittääkseni käytetään monissa karttasovelluksissa, joissa myös pelataan viivoilla ja vektoreilla.
- Liittynyt
- 06.11.2016
- Viestejä
- 954
Täällä varmaan Reactin taitajia.
Netissä löytyy ihan valtavasti matskua ja ohjeita että miten React tai React Nativella saadaan fetchilla tai axiosilla haettua websivun JSON dataa, mutta en kyllä meinaa löytää yhtään mitään järkevää että mitä vastaavasti pitäisi tehdä kun fetch ei palautakaan JSONia vaan HTML:lää? JSONista on äärimmäisen helppo parsia haluamaansa dataa, mutta toi HTML mikä sieltä palautuu niin minulla ei ole mitään käsitystä mitä sen kanssa pitäisi tehdä.
Minun pitäisi saada liiketoiminnan eperusteiden ePerusteet haettua tiettyjä asioita yhtä koulun React Native projektia varten, mutta en tosiaan tiedä yhtään mitä tuon sekavan HTML-litannian kanssa pitäisi tehdä minkä fetch palauttaa. Huom. response.json() ei toimi tässä, sillä tulee "JSON Parse error: Unrecognized token '<' ", eli pitää olla tuossa response.text() muodossa.
Koodi.
Ja console.log palauttama data siitä mitä dataa websivulta saatiin haettua:
Netissä löytyy ihan valtavasti matskua ja ohjeita että miten React tai React Nativella saadaan fetchilla tai axiosilla haettua websivun JSON dataa, mutta en kyllä meinaa löytää yhtään mitään järkevää että mitä vastaavasti pitäisi tehdä kun fetch ei palautakaan JSONia vaan HTML:lää? JSONista on äärimmäisen helppo parsia haluamaansa dataa, mutta toi HTML mikä sieltä palautuu niin minulla ei ole mitään käsitystä mitä sen kanssa pitäisi tehdä.
Minun pitäisi saada liiketoiminnan eperusteiden ePerusteet haettua tiettyjä asioita yhtä koulun React Native projektia varten, mutta en tosiaan tiedä yhtään mitä tuon sekavan HTML-litannian kanssa pitäisi tehdä minkä fetch palauttaa. Huom. response.json() ei toimi tässä, sillä tulee "JSON Parse error: Unrecognized token '<' ", eli pitää olla tuossa response.text() muodossa.
Koodi.
Ja console.log palauttama data siitä mitä dataa websivulta saatiin haettua:
Mitä sinun siis pitäisi lukea? Parseroida? Kokeile vaikka näillä ohjeilla: Parse HTML in JavaScript.
- Liittynyt
- 06.11.2016
- Viestejä
- 954
Joo, joukosta pitäis parsia Liiketoiminnan eperusteiden ammatilliset ja yhteisopinnot sekä niiden opintopistemäärät. Jotain noita HTLM-parsereita jo testailinkin pääsemällä niissä yhtään sen pitemmälle. Nyt ei kyllä kuuppa kestä enää tälle päivälle yhtään enempää, olen aamu ysistä asti nököttänyt tässä koneen äärellä tätä ihmetellen. Nyt lähden hakemaan kaupasta megapussin sipsiä vitutukseen.
Lisähauskuuttahan tuossa tuo vielä se, että suoraan HTML:n joukossa ei ole noita asioita mitä pitäisi sieltä kaivaa vaan ne taas tulee sivulle javascriptillä, joten pelkästään sivun HTML:n hakeminen ei vielä riitä. Tuollaisten sivujen parsiminen on muutenkin aika hanurista.
Samaa olin tulossa sanomaan, että ei noita tietoja tuolta sivulta palautuvasta HTML:stä ole parsittavissa.
Kiinnostaisi nähdä tarkka tehtävänanto. Kuulostaa vähän epätavalliselta koulutehtävältä, jos tuon urlin kautta pitäs saada parsituksi nuo mainitut.
Kiinnostaisi nähdä tarkka tehtävänanto. Kuulostaa vähän epätavalliselta koulutehtävältä, jos tuon urlin kautta pitäs saada parsituksi nuo mainitut.
totallynotrobot
Tukijäsen
- Liittynyt
- 09.02.2019
- Viestejä
- 815
En tunne eperusteet-sivua yhtään, mutta ettei tässä olisi tarkoitus käyttää heidän apia? Jonkinlainen tuntuisi löytyvän: ePerusteet julkiset rajapinnat - Opintopolun palvelukokonaisuus - Eduuni-wiki
- Liittynyt
- 17.10.2016
- Viestejä
- 15 883
Tämä. Olisiko kuitenkin tarkoitus käyttää jotain APIa? HTML:n parsiminen tuolla tavalla on muutoinkin ihan viimeinen oljenkorsi ja hajoaa loputtoman helposti heti kun mitä tahansa muutetaan siellä sivulla. Saati jos se data ei edes tule suoraan HTML:ssä, vaan vaatii skriptin ajamista.
- Liittynyt
- 06.11.2016
- Viestejä
- 954
Ei ole varsinainen "koulutehtävä", vaan kurssilla piti löytää kummiyritys tai vastaavaa jolle ryhmäprojektina voidaan toteuttaa kummiyrityksen toivoma aplikaatio tai websivu tai vastaavaa. Minun 3-hengen ryhmällä on tarkoitus tehdä mobiiliappi liiketoiminnan opiskelijoiden käyttöön, jolla opiskelija voi drag & drop laatikoita vetämällä koostaa oman henkilökohtaisen opetussuunnitelmansa ja esittää tämän vastuuopettajalleen. Näihin vedettäviin laatikoihin olisi tarkoitus eperusteista saada opinnot ja opintoisteiden määrä, ja kyseisiä laatikoita voi vetää lukukauden 5-jakson periodeihin (kesä on se viides) niin että jokaisella periodilla näkyy siihen koottujen opintojen opintopisteiden määrä.
Toistaseksi olen saanu vetolaatikot ja periodizonet toimimaan ja ajattelin seuraavaksi perehtyä siihen että miten saan tuolta eperusteista tarvittavan datan pihalle, mutta näemmä en saa ainakaan kyseistä sivua parsimalla.
Joo, APIa on tarkoitus käyttää. On vain koko React ja webhomma itselle vielä ihan uusi juttu, että en ole ihan perillä näistä. Kovaa touhua kun ensimmäinen lukuvuosi opetettiin Pythonia ja C#, joiden ylimääräiseen opiskeluun panostin myös omalla ajallani ihan hemmetisti. Sitten tokan lukuvuoden alussa heitetään tekemään "asiakkaalle" ohjelmaa rajapintaan Reactilla, joka pitäis siinä tekemisen ohessa samalla opetella. Olisivat voineet opettajat vaikka hyvissä ajoin vinkata että tämmöstä tulossa, mutta ei. Tässä painanut ohessa Moocin Fullstack Open-kurssia jossa käydään isommin Reactia, Mongo DB:tä ja muuta mukavaa.
Viimeksi muokattu:
Juu, tiedän kyllä tuon tuskan. Aikanaan tartti yliopistolla yhdellä kurssilla opetella lennosta Python + Flask, HTML ja Javascript + JQuery ja koodaileen semmonen full stack web-sovellus aika nopsalla aikataululla, niin olihan se aika raskas paketti yhdellä kertaa. SQLite tais olla kantana. Toki kurssilla oletettiin, että tuo fronttipuoli (eli HTML ja Javascript) ois ollu jollain tasolla entuudestaan tuttua, mutta ei ollu aikaa käydä esitietokursseja
Mutta tuollaista se voi olla sit duunissakin, että lennosta joutuu opettelemaan asioita ja siihen joutuu vähän niin kuin tottumaan.
Tuosta itse keissistä, niin ihan nopealla vilkaisulla tuo API-dokkari ylempänä ei kerro, miten kyseiseen API:in pitää tunnistautua. Tunnistautuminen sun tarvii selvittää ihan ekana, koska oletan, että jos heittelet suorilta vaan kutsua sinne ilman asiaankuuluvaa autentikaatiota, niin se vastailee, että pääsy kielletty.
Mut jos teillä on vaan jossain ohjeet, miten tuonne autentikoidutaan, niin sitten esim. jonkun autentikaatioheaderin lisäys tuonne Reactiin ei oo kummoinen juttu. Se kannattaa toki selvittää itselleen, että mikä on hyvä tapa käsitellä salaisuuksia (salasanat, privaattiavaimet, API-tokenit ja sen sellaiset) sovelluksessa ja sanon, vaikka voi olla itsestään selvää, että tunnarien kovakoodaaminen koodiin ei ole.
muoks. äh, olkoon tuossa ylemmät, mutta jos nää julkiset rajapinnat tarjoaa tarvittavan tiedon, niin edelliset autentikaatiolätinät voi unohtaa: ePerusteet julkiset rajapinnat - Opetushallituksen palvelukokonaisuus - Eduuni-wiki
Noi on siis nimensä mukaisesti kaikille auki.
Viimeksi muokattu:
Kiitos näistä. Tuli törmättyä myös tähän Plans and pricing : PythonAnywhere
mikä saattaisi olla hyvä tai ehkä jopa paras vaihtoehto omiin tarpeisiin
Uutiset
-
Huippuylikellottaja Splave lähtee mukaan komponenttimarkkinoille Enermaxin ja G.Skillin tukemana
10.1.2025 05:04
-
Asus julkaisi joukon uusia AIO-coolereita sekä päivitti NUC-malliston vuoteen 2025
10.1.2025 04:38
-
Yhdysvaltoihin markkinoitaan laajentava Endorfy mukana CES-messuilla
9.1.2025 18:41
-
Thermaltake esitteli CES-messuilla uusia ajosimulaattorituotteita
9.1.2025 16:34
-
InWin esitteli CES-messuilla näyttävän PRISM-kotelon ja avonaisen SHIFT-testipenkin
9.1.2025 03:13
