Kuntavaalit 2021

[Johan_V]

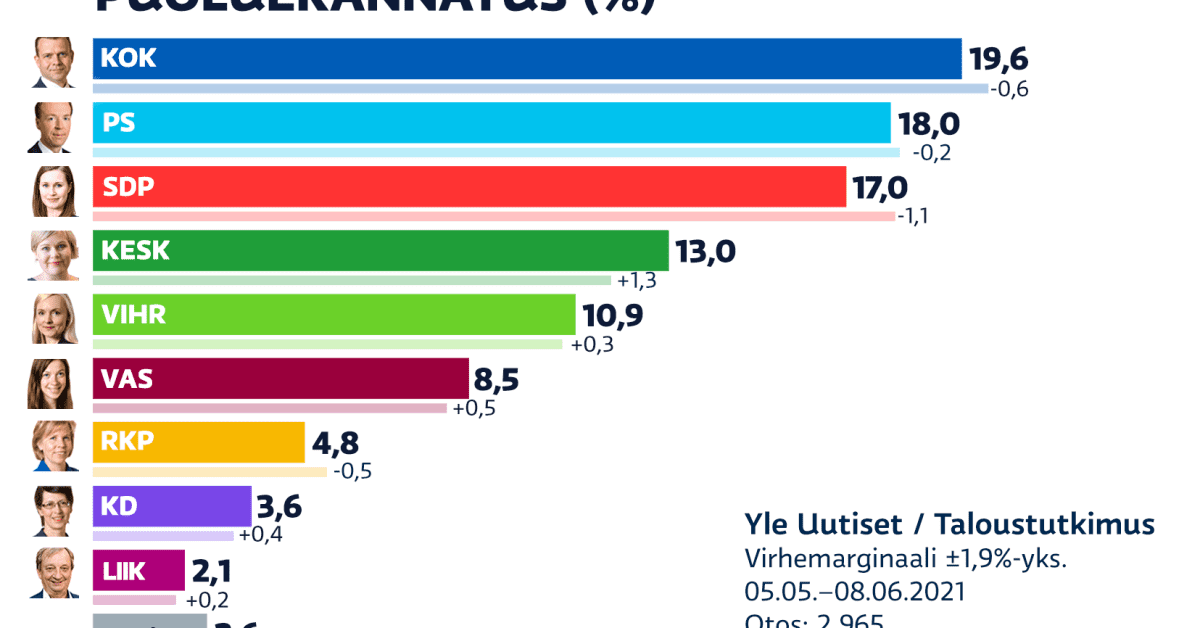
No ei kyllä tarkoita. Tuo on valitettavan yleinen ja väärä harha ja tekee virheellisen oletuksen jakaumasta. Kuten sanoin, gallupin tulos ei ole tasainen jakauma. Koska tämä sama asia tulee jatkuvasti eteen, niin laitan vaikka ulkoisen lähteen:

Mikä on virhemarginaali?

Tilastotieteilijät käyttävät tutkimuksissaan todennäköisyyslaskentaa.

yle.fi

Eli jos gallup antaa puolueen kannatukseksi 20% ja virhemarginaaliksi 2% suuntaansa, on (noin) 20% kannatus paljon todennäköisempi kuin (noin) 18% tai 22% kannatus. Tai vaikka 5% tai 35% kannatus. Jälkimmäisetkin ovat mahdollisia, mutta aina vaan epätodennäköisempiä. Ehkä ihmiset tajuaisivat asian helpommin, jos tuo virhemarginaali esitettäisiin jakaumana: keskeltä korkea, reunoilta matala. Sitten siitä voi valita ihan oman luottamusvälin ja sen saa juuri niin leveäksi tai kapeaksi kuin haluaa ja avautuu ehkä helpommin että se gallupin tulos on se todennäköisin.

Ja sama käy ilmi Wikistä kun huomaat, miten jakauman pinta-ala muuttuu eri luottamusvälien (95%, 99% jne.) mukaan. Virhemarginaali on siis myös täysin riippuvainen valitusta luottamusvälistä. 99,999999% luottamusvälillä se virhemarginaali on karkeasti mitä tahansa 0 ja 100% välillä. Tai 1% luottamusvälillä se on hyvin hyvin kapea kaistale sen gallupin tuloksen ympärillä ja mikään puolue ei ole toisensa kanssa päällekäin. Yleensä käytetään 95%:a mutta myös muita tilanteesta riippuen.

Margin of error - Wikipedia

en.wikipedia.org

Alkaa menemään OFFTOPICin puolelle, mutta tuo ylen artikkeli osoittaa kuinka vaikeaa perinteistä tilastotiedettä on ymmärtää.
Kerrataan nyt vielä: Tuo on nimenomaan väärä tulkinta. Tilastoanalyysissä kannatusprosentti ei ole tilastollinen muuttuja, vaan tuntematon vakio. Ei sillä voi olla todennäköisyysjakaumaa. Se mitä luottamusväli tarkoittaa on se että jos gallup toistetaan monta kertaa ja luottamusväli lasketaan, niin 95% tapauksista luottamusväli sisältää "oikean" kannatuksen.

 

[Paapaa]

Kerrataan nyt vielä: Tuo on nimenomaan väärä tulkinta. Tilastoanalyysissä kannatusprosentti ei ole tilastollinen muuttuja, vaan tuntematon vakio. Ei sillä voi olla todennäköisyysjakaumaa.

Tossa nyt ei ole mitään järkeä. Ei se jakauma liity siihen todelliseen kannatukseen (joka on vakio), vaan siihen, että me saadaan se todellinen kannatus satunnaisotannalla selville kun kysytään tarpeeksi suurelta joukolta. Se ei ole (tietenkään) tasainen/olematon jakauma. Vaan kun me toistetaan se samplaus monta kertaa, me saadaan suurimman osan ajasta lähelle oikeaa tulosta, ja harvemmin kauemmaksi. Ja vielä harvemmin ihan helvetin kauaksi. Ei ole mitään 4 prosentin aluetta, jonka tulokset tulevat aina samalla todennäköisyydellä ja sen ulkopuolella sitten jollain pienemmällä tasaisella/olemattomalla todennäköisyydellä, vaikka niin näytät kuvittelevan. Ja ehkä yhden kerran miljoonasta se tulos on ihan älytön, sekin on mahdollista mutta hyvin epätodennäköistä. Näistä kun tehdään jakauma, se on öbaut normaalijakauma, ei tasainen jakauma, ei mitään jyrkkiä reunoja kuten kuvittelet.

Kuvitelmasi tasaisesta (tai olemattomasta) jakaumasta on ihan älytön, enkä oikein keksi mistä sen olet oikein tempaissut. Vai olemmeko samaa mieltä että normaalijakauma (tai binomijakauma isolla N:llä) on järkevä oletus gallupin tuloksille? (Ja jos olet samaa mieltä, olet ihan määritelmän mukaan väärässä virhemarginaalista. Eli vastaat mitä tahansa, niin metsään menee.)

Se mitä luottamusväli tarkoittaa on se että jos gallup toistetaan monta kertaa ja luottamusväli lasketaan, niin 95% tapauksista luottamusväli sisältää "oikean" kannatuksen.

Kyllä, mutta ei tasaisesti. Jakauma on likimäärin normaalijakauma. Esim. puolueen kannatus on gallupissa 20% ja virhemarginaali on 2% suuntaansa 95%:n luottamusväillä. Sen kannatus voi olla oikeastaan mitä tahansa 0:n ja 100:n välillä (ei-inkusiivinen), mutta mitä kauemmaksi mennään tuloksesta, sitä epätodennäökisemmin se on oikea arvo. Ei ole mitään tasaisen jakauman aluetta, vaan enemmän tai vähemmän normaalijakauma.

Laitan sulle lisää näitä, jos vaikka ymmärtäisit niiden avulla paremmin kun en itse näköjään osaa:

Todennäköisyys sille, että todellinen kannatusluku osuu kuvion keskellä olevalle tummennetulle alueelle on kussakin tapauksessa n. 4 % ja pienenee siitä etäännyttäessä.

Puoluekannatus ja virhemarginaalit – Informaatiomuotoilu.fi

informaatiomuotoilu.fi

Lause on muodollisesti totta, mutta erittäin harhaanjohtava. Kaikki arvot virhemarginaalin sisällä eivät nimittäin ole yhtä todennäköisiä vaan todennäköisimmät arvot ovat juuri ilmoitetun kannatuksen (25,9 prosenttia) kohdalla ja vieressä. Marginaalin äärimmäiset arvot 22,9 ja 28,9 ovat jo melko epätodennäköisiä.

Viimeisimmät gallupit lupaavat huippujännittävää vaali-iltaa

Vihreät on mielipidemittausten perusteella tukevasti valtakunnan neljänneksi suurin puolue sunnuntaina järjestettävien kuntavaalien alla.

www.vihrealanka.fi

"This poll says 53-47 but its margin of error is 4.2 points. It might just as easily be 49-51 or 57-43. What a useless poll!"

The problem here is the "just as easily". All else being equal, polls will follow a bell-curve distribution, meaning that while the results that are close to the poll's MOE away from the result are within the 95% confidence range, they're also a lot less likely than values closer to the actual poll result. Assuming this poll was all we knew about a race and the poll was perfectly conducted, there would still be a 92% chance that the party shown as ahead by the poll was indeed ahead.

"Margin Of Error" Polling Myths

Tasmanian and Australian psephology, opinion poll analysis, election analysis and political commentary by Dr Kevin Bonham.

kevinbonham.blogspot.com

Auttaisko noi sua ymärtämään, että ei ole mitään +/-2 prosentin tasaista aluetta, jonka kaikki arvot ovat yhtä todennäköisiä?

 

[Johan_V]

Kyllä, mutta ei tasaisesti. Jakauma on likimäärin normaalijakauma. Esim. puolueen kannatus on gallupissa 20% ja virhemarginaali on 2% suuntaansa 95%:n luottamusväillä. Sen kannatus voi olla oikeastaan mitä tahansa 0:n ja 100:n välillä (ei-inkusiivinen), mutta mitä kauemmaksi mennään tuloksesta, sitä epätodennäökisemmin se on oikea arvo. Ei ole mitään tasaisen jakauman aluetta, vaan enemmän tai vähemmän normaalijakauma.

En nyt jaksa tästä enempää vääntää, mutta mikä jakauma? Kysymys on siitä mitä näyte kertoo populaatiosta. Tässä generoidaan luottamusvälejä, ei pistearvioita. Toki voit approksimoida binomijakaumaa normaalijakaumalla, mutta sillä ei tämän asian kanssa mitään tekemistä.

 

[Paapaa]

En nyt jaksa tästä enempää vääntää, mutta mikä jakauma? Kysymys on siitä mitä näyte kertoo populaatiosta. Tässä generoidaan luottamusvälejä, ei pistearvioita. Toki voit approksimoida binomijakaumaa normaalijakaumalla, mutta sillä ei tämän asian kanssa mitään tekemistä.

Galluptulosten jakauma, taisin tämän jo kirjoittaa aiemmin. Kun me samplataan, me saadaan joka kerralla vähän eri tulos. Ne tulokset noudattavat (normaali-)jakumaa sen todellisen kannatuksen ympärillä niin, että useimmin saadaan gallupista tulos joka on lähellä oikeaa kannatusta ja harvemmin tulos joka on kauempana oikeasta kannatuksesta. Se on normaalijakauma ja sen voit helposti simuloida vaikka Pythonilla (binomijakaumalla: henkilö vastaa 20% todennäköisyydellä kannattavansa puoluetta X), rinse and repeat. Lopputuloksena saat niille usealle riippumattomalle gallupille normaalijakauman, et tasaista jakaumaa, kuten ilmeisesti väität. Virhemarginaalie ei ole tällaisessa samplauksessa tasainen pötkö, vaan saat useammin lähellä oikeaa kannatusta olevan tuloksen -> normaalijakauma.

Ja koska näistä lukemattomista gallupeista suurin osa sijoittuu lähelle todellista kannatusta, on satunnaisen gallupin antama keskiarvo todennäköisemmin myös oikea kannatus kuin kaukana keskiarvosta oleva tulos.

 

[Johan_V]

Galluptulosten jakauma, taisin tämän jo kirjoittaa aiemmin. Kun me samplataan, me saadaan joka kerralla vähän eri tulos. Ne tulokset noudattavat (normaali-)jakumaa sen todellisen kannatuksen ympärillä niin, että useimmin saadaan gallupista tulos joka on lähellä oikeaa kannatusta ja harvemmin tulos joka on kauempana oikeasta kannatuksesta. Se on normaalijakauma ja sen voit helposti simuloida vaikka Pythonilla (binomijakaumalla: henkilö vastaa 20% todennäköisyydellä kannattavansa puoluetta X), rinse and repeat. Lopputuloksena saat niille usealle riippumattomalle gallupille normaalijakauman, et tasaista jakaumaa, kuten ilmeisesti väität. Virhemarginaalie ei ole tällaisessa samplauksessa tasainen pötkö, vaan saat useammin lähellä oikeaa kannatusta olevan tuloksen -> normaalijakauma.

Ja koska näistä lukemattomista gallupeista suurin osa sijoittuu lähelle todellista kannatusta, on satunnaisen gallupin antama keskiarvo todennäköisemmin myös oikea kannatus kuin kaukana keskiarvosta oleva tulos.

Niin tämä on Bayesialainen tulkinta, mikä on oikein, ja tästä saadaan Bayesilainen luottamusväli. Mutta tämä on eri asia kuin perinteisen tilastotieteen luottamusväli.

 

[Paapaa]

Niin tämä on Bayesialainen tulkinta, mikä on oikein, ja tästä saadaan Bayesilainen luottamusväli. Mutta tämä on eri asia kuin perinteisen tilastotieteen luottamusväli.

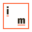
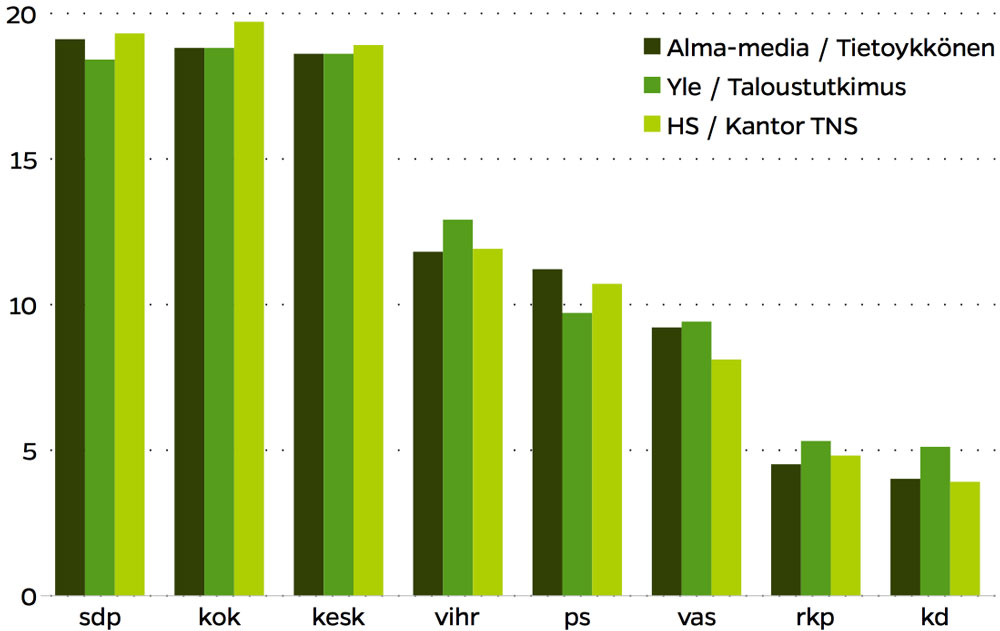
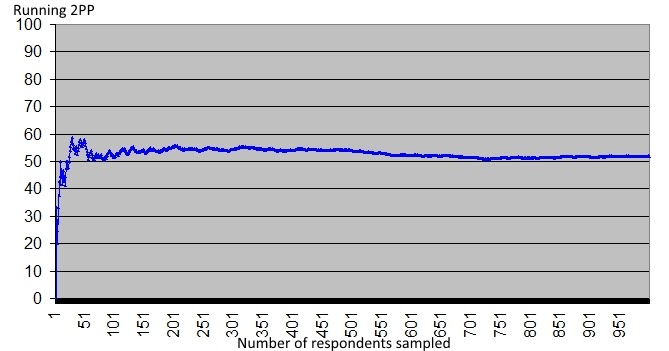
Sulla kuule taitaa olla ihan Johan_V:n itse keksimä tilastotiede nyt käytössä Pidä se ihan omana tietonasi, sillä ei ole mitään tekemistä gallupien tulosten tulkinnan kanssa. Lähteet ja perustelut olenkin jo kirjoittanut.

 

[taxman]

Alkaa menemään OFFTOPICin puolelle, mutta tuo ylen artikkeli osoittaa kuinka vaikeaa perinteistä tilastotiedettä on ymmärtää.
Kerrataan nyt vielä: Tuo on nimenomaan väärä tulkinta. Tilastoanalyysissä kannatusprosentti ei ole tilastollinen muuttuja, vaan tuntematon vakio. Ei sillä voi olla todennäköisyysjakaumaa. Se mitä luottamusväli tarkoittaa on se että jos gallup toistetaan monta kertaa ja luottamusväli lasketaan, niin 95% tapauksista luottamusväli sisältää "oikean" kannatuksen.

Frekventistisesti noin, mutta Bayesilaiset ovat paljon onnellisempisia elämässään

edit: Kas, Johan olikin jo ymmärtänyt asian.

 

[samiv]

Itse en oikein ymmärrä että miksi joku ei kävisi äänestämässä ennakkoon, jos ylipäänsä aikoo äänestää. Paljon helpommalla sitä pääsee, kun on enemmän varaa valita äänestyspaikan suhteen eikä tarvi ahtautua vaalipäivänä muiden kanssa ruuhkaan.

Varsinainen äänestyspaikka on paljon lähempänä kuin ennakkoäänestys. Miksi ihmeessä menisin jonnekin vitunaikaiseen peltomarkettiin täältä kaupunkialueelta, vain jotta voisin äänestää.

 

[pekka666]

Varsinainen äänestyspaikka on paljon lähempänä kuin ennakkoäänestys. Miksi ihmeessä menisin jonnekin vitunaikaiseen peltomarkettiin täältä kaupunkialueelta, vain jotta voisin äänestää.

Jaa kai Oulu on sitten jotenkin poikkeus kun täällä niitä paikkoja on ihan keskustassakin

 

[Naamapalmu]

Ylen kuntavaalimittaus:
Kok 19,6
Ps 18,0
Sdp 17,0
Kesk 13,0

Kokoomus on myös Ylen kuntavaalimittauksen mukaan lähdössä ennakkosuosikkina kuntavaaleihin. Toisena tulevien perussuomalaisten äänestysvarmuus on kysymysmerkki, eli paljon riippuu siitä, kuinka he saavat aktivoitua äänestäjiään vaaliuurnille varsinaisena vaalipäivänä. Sdp:n kannatus taas näyttäisi sulavan Ylen kuntavaalimittauksen mukaan, verrattuna HS:n tekemään gallupiin. Keskusta on Ylen kuntavaalimittauksen mukaan suurin nousija, Saarikon hyvä esiintyminen kuntavaalitenteissä on tuonut nostetta keskustalle.

 

[Disfear]

En nyt tiedä menenkö täysin metsään, ja vähän olen typerästi vain stereotypioiden varassa, mutta voisin kuvitella, että perussuomalaisten kannattajista suhteessa suurempi osa on liikkeellä vaalipäivänä. Ellei sitten ole päässyt käymään niin, että nykypolitiikkaan tyytymättömät ovat niin tyytymättömiä, että tavallaan poikkeuksellisesti ovat päättäneet lähteä uurnille jo ennakkoon.

Paha sanoa, mutta ainakin perinteisesti perussuomalaisten kannattajissa on melko paljon ns. duunariäänestäjiä, ja omassa pienen otannan tuttavapiirissäni sellainen keskimääräinen duunari ehkä käy ennemmin vaalipäivänä äänestämässä, eikä välttämättä ole tyypillisesti noteerannut mahdollisuutta äänestää ennakkoon.

Toisaalta perussuomalaiset ovat ilmeisesti nostaneet kannatusta entistä koulutetuimpien ihmisten keskuudessa, joten kai tuo äänestyskäyttäytyminen voi olla yhtäläistä muiden puolueiden kanssa. Jos nyt edes äänestyskäyttäytymisellä ja koulutustaustalla lopulta on niin isoa merkitystä tässä suhteessa.

 

[Varistin]

En nyt tiedä menenkö täysin metsään, ja vähän olen typerästi vain stereotypioiden varassa, mutta voisin kuvitella, että perussuomalaisten kannattajista suhteessa suurempi osa on liikkeellä vaalipäivänä. Ellei sitten ole päässyt käymään niin, että nykypolitiikkaan tyytymättömät ovat niin tyytymättömiä, että tavallaan poikkeuksellisesti ovat päättäneet lähteä uurnille jo ennakkoon.

Paha sanoa, mutta ainakin perinteisesti perussuomalaisten kannattajissa on melko paljon ns. duunariäänestäjiä, ja omassa pienen otannan tuttavapiirissäni sellainen keskimääräinen duunari ehkä käy ennemmin vaalipäivänä äänestämässä, eikä välttämättä ole tyypillisesti noteerannut mahdollisuutta äänestää ennakkoon.

Toisaalta perussuomalaiset ovat ilmeisesti nostaneet kannatusta entistä koulutetuimpien ihmisten keskuudessa, joten kai tuo äänestyskäyttäytyminen voi olla yhtäläistä muiden puolueiden kanssa. Jos nyt edes äänestyskäyttäytymisellä ja koulutustaustalla lopulta on niin isoa merkitystä tässä suhteessa.

Uskoisin että tänä vuonna myös vaalien ajankohta vaikuttaa aika lailla yleiseen ennakkoäänestysintoon. Itse kävin tiistaina äänestämässä ennakkoon, kun tajusin että aion sunnuntaina olla ihan jossain muualla kuin kotipaikkakunnalla, eikä kiinnosta kiirehtiä kotiin vain että ehtisi uurnalle. Tuli samalla mieleen, että miten monelle äänestyksen varsinaiselle vaalipäivälle jättäneistä mahtaa tulla tämä valaistuminen liian myöhään, eli tajutaan sunnuntaina mökillä / lomamatkalla / muussa kesäriennossa, että äänestyskin olis.

 

[ATE]

Näytti vähän pahalta sään suhteen Helsingissä ja muualla Eteläsuomessa mutta nyt näyttää säätiedotus muutamaa tippaa aamupäivällä ja ihan yksittäisiä tippoja päivällä mutta sitten näyttää olevan puolipilvistä ja suht optimaalinen sää ulkoiluun.

 

[Viinasta]

Noniin. Joko on nessut ja sampat valmiina?

 

[Lacsative]

Noniin. Joko on nessut ja sampat valmiina?

Ei, hirveä krapula ja helvetillinen helle kämpässä. Tähän vielä Persujen vaalivoitto niin kyllä lähtee.

 

[Paapaa]

Sää ei ainakaan ole äänestysintoa laskenut, mikä on hyvä asia. Ja peli auki, ennakkoäänet julki!

Kok 21,0
SDP 18,4
Kesk 16,9
PS 13,5
Vihr 9,6
Vas 8,5
RKP 4,6
KD 3,8
Liik 1,2

Ehtii toki muuttua vaikka mihin vielä. Keskusta ainakin tyypillisesti putoaa. PS saattaisi nousta vaalipäivän äänillä. Ja PS on hyvin luultavasti - kuten ennakoitiin - vaalien kovin kannatuksen kasvattaja.

 

[PalleX]

Jytky tais jäädä lussuksi.

 

[hoppa]

Näkeekö jostain tuloslaskentaa kunnittain?
edit: löytyi.

Koko maa, tulokset

 

[Paapaa]

Näkeekö jostain tuloslaskentaa kunnittain?

Yle - Tulospalvelu - Koko maa - Kuntavaalit 2021 - Yle.fi

Tarkastele vaalitulosta kunnittain, kunnan äänestysalueittain tai koko maan tasolla.

vaalit.yle.fi

Tai:

Etusivu

 

[Jurppii]

Halla-ahokin voi jo rohkeasti lupailla, että lähtisi varapormestariksi kun PS Helsingissä turvallisesti kuudennella sijalla.

 

[Paapaa]

Halla-ahokin voi jo rohkeasti lupailla, että lähtisi varapormestariksi kun PS Helsingissä turvallisesti kuudennella sijalla.

Vähän ehkä yllättävä toi PS:n tulos Helsingissä. Tällä hetkellä +/- 0 paikkaa PS:lle. Tai jotenkin olin kuvitellut, että Halla-aho repisi missä tahansa Jeesus-äänisaaliin. Mutta ei välttämättä pärjää Valtonen-Vartiainen -kaksikolle.

 

[Tommy Goldfish]

Ylen lähetyksestä äsken kuultua: Pääministeri Marin on ylen pihalla jo.

Ennakkotulokset tuli ja alkoi kupitus?

 

[Naamapalmu]

Keskustalle torjuntavoitto, vaikka tulos tulee laskemaan. Kokoomuksen osalta aika odotettu tulos, tuleeko vaalivoitto huonoimmalla tuloksella 30 vuoteen? (kiikun kaakun) SDP:n tulos yllätti, suurempi mitä odotin. PS suurin nousija, mutta tulos on toistaiseksi lievä pettymys kaiken gallup-tuloksien jälkeen.

 

[shaminy]

Ei tullu Jytkyä
Valtamedia jälleen väärensi galluppeja Persujen hyväksi.

 

[Paapaa]

Ei tullu Jytkyä
Valtamedia jälleen väärensi galluppeja Persujen hyväksi.

Vantaalla PS:lle soviteltiin jopa toiseksi suurimman puolueen viittaa ja 20%:n kannatusta. Nyt kannatus 16,5%. Eli yllättävän kaukana vielä gallup-luvuista. Mutta, ilta on nuori. Kokoomus menossa demarien ohi. Mutta tällä hetkellä lähes tasoissa.

 

[inexcess]

Jokaiselle joka on politiikkaa seurannut viimeiset 10 vuotta, on ollut selviö ettei Perussuomalaisten 18-19% kuntavaalikannatus realisoidu.

Kuntavaalit on monille äänestäjille paikallisvaali ja myös henkilövaali. Persuilla ei ole useimmilla paikkakunnilla tarjota tunnettuja ja pidempään politiikassa vaikuttaneita hahmoja. Tämän näkee hyvin Helsingissä, jossa Halla-ahon äänisaalis tällä hetkellä +5000 ääntä seuraavien tuntemattomien jäädessä vaivaiseen pariin sataan.

 

[inexcess]

Jatkan vielä...

Jos unohdetaan prosentit ja katsotaan tulossa olevia kunnanvaltuustopaikkoja, jotka ovat ne oikeasti merkityksellinen asia, niin aika kova tulos Persuille on tulossa verrattuna edellisiin kunnallisvaaleihin (58,8% laskettu):
Kok: 1531 (+41 paikkaa verrattuna vuoteen 2017)
SDP: 1493 (-204 paikkaa verrattuna vuoteen 2017)
Kesk: 2475 (-349 paikkaa verrattuna vuoteen 2017)
PS: 1249 (+499 paikkaa verrattuna vuoteen 2017)

 

[Tohelo]

Mikähän idea tuossa on takana kun Yle näyttää puolueet järjestyksessä äänestys% mukaan, mutta maikkari laittaa vihreät persujen edelle?

Disclaimer: En kannata kumpaakaan vihr/ps.

 

[JCSH]

Jokaiselle joka on politiikkaa seurannut viimeiset 10 vuotta, on ollut selviö ettei Perussuomalaisten 18-19% kuntavaalikannatus realisoidu.

Kuntavaalit on monille äänestäjille paikallisvaali ja myös henkilövaali. Persuilla ei ole useimmilla paikkakunnilla tarjota tunnettuja ja pidempään politiikassa vaikuttaneita hahmoja. Tämän näkee hyvin Helsingissä, jossa Halla-ahon äänisaalis tällä hetkellä +5000 ääntä seuraavien tuntemattomien jäädessä vaivaiseen pariin sataan.

Eiköhän tuohon vaikuta myös aika paljon se että Persujen linjaukset kunnallispolitiikan kannalta relevanteissa asioissa ovat olleet aika laihoja. Tai jos eivät laihoja niin sitten vähintäänkin ristiriitaisia.
Oikein nauratti kun yhden persujen kuntavaalimainoksessa luki käytännössä vain isolla "MAAHANMUUTTO!" (tai voi olla että siinä luki jotain muutakin mutta ei oikein autosta ohiajaessa ehtinyt lukeen tarkemmin) ja ajattelin että onpa helvetin relevantti slogani Tampereen kaupunginvaaleissa

 

[Naamapalmu]

Vihreiden todella heikko tulos kyllä yllättää samalla tavalla kuin keskustan kannatus.

 

[inexcess]

Eiköhän tuohon vaikuta myös aika paljon se että Persujen linjaukset kunnallispolitiikan kannalta relevanteissa asioissa ovat olleet aika laihoja. Tai jos eivät laihoja niin sitten vähintäänkin ristiriitaisia.
Oikein nauratti kun yhden persujen kuntavaalimainoksessa luki käytännössä vain isolla "MAAHANMUUTTO!" (tai voi olla että siinä luki jotain muutakin mutta ei oikein autosta ohiajaessa ehtinyt lukeen tarkemmin) ja ajattelin että onpa helvetin relevantti slogani Tampereen kaupunginvaaleissa

Maahanmuutto on Tampereen kaltaisessa kaupungissa sinänsä relevantti kunnallisvaaliteema, että jos sitä ei hillitä, muuttuu Tampere Malmön ja Göteborgin lailla osittain asumiskelvottomaksi kaupungiksi. Kannattaisi kuitenkin miettiä sitä, miten tämän teeman tuo julki.

Persuissa pitäisi ymmärtää myös se, että maahanmuutto ja EU-kriittisyys ei kanna kunnallisvaaleissa johtopaikoille. Ongelma on ollut se, että kokonaisuutena Persujen kunnallisiin toimintoihin vaikuttava teema on jäänyt epäselväksi. Jopa minulle joka seuraa politiikkaa.

 

[Jurppii]

Maahanmuutto on Tampereen kaltaisessa kaupungissa sinänsä relevantti kunnallisvaaliteema, että jos sitä ei hillitä, muuttuu Tampere Malmön ja Göteborgin lailla osittain asumiskelvottomaksi kaupungiksi. Kannattaisi kuitenkin miettiä sitä, miten tämän teeman tuo julki.

No tuskin sitä kuitenkaan kaupunginvaltuustosta käsin asiaan vaikutetaan.

 

[KeljuK]

Ongelma on ollut se, että kokonaisuutena Persujen kunnallisiin toimintoihin vaikuttava teema on jäänyt epäselväksi. Jopa minulle joka seuraa politiikkaa.

Täällä omassa kotikaupungissa pääkaupunkiseudulla tuntui eka teema olevan se että vaikka kuinka yritti hakea niin nk. kunta-asioista kiinnostuneilla ehdokkailla ei ollut yhtään mitään nettinäkyvyyttä, eli hakemallakaan ei löhytänyt edes Facesivua jossa kertoisi kuntavaaliteemoistaan tai keskustelisi kunnan asioista. Erittäin moni vihr/kok/dem ehdokas, varsinkin vihr/kok oli nyt sentään vaivautunut pistämään jonkun puolikkaan A4:n kokosen blogin/kotisivun johon on kirjoittanut ajatuksiaan.
Mut "Ville, eläkeläinen, putkimies. Kunta kuntoon" ei nyt oikein mun mielestä kerro yhtikäs mitään mitä ehdokas ajattelee kunnan asioista saatikka niille tekevänsä.

 

[shaminy]

Täällä omassa kotikaupungissa pääkaupunkiseudulla tuntui eka teema olevan se että vaikka kuinka yritti hakea niin nk. kunta-asioista kiinnostuneilla ehdokkailla ei ollut yhtään mitään nettinäkyvyyttä, eli hakemallakaan ei löhytänyt edes Facesivua jossa kertoisi kuntavaaliteemoistaan tai keskustelisi kunnan asioista. Erittäin moni vihr/kok/dem ehdokas, varsinkin vihr/kok oli nyt sentään vaivautunut pistämään jonkun puolikkaan A4:n kokosen blogin/kotisivun johon on kirjoittanut ajatuksiaan.
Mut "Ville, eläkeläinen, putkimies. Kunta kuntoon" ei nyt oikein mun mielestä kerro yhtikäs mitään mitä ehdokas ajattelee kunnan asioista saatikka niille tekevänsä.

Tuota minäkin ihmettelin, ja kyselin myös muutamalta ehdokkalta miksei ole kotisivuja. Vastaukseksi sain että "tule kysymään hekilökohtaisesti niin voin vastata". Ei tuo ole tätä päivää.

 

[JCSH]

Maahanmuutto on Tampereen kaltaisessa kaupungissa sinänsä relevantti kunnallisvaaliteema, että jos sitä ei hillitä, muuttuu Tampere Malmön ja Göteborgin lailla osittain asumiskelvottomaksi kaupungiksi. Kannattaisi kuitenkin miettiä sitä, miten tämän teeman tuo julki.

Ei tuo siitä relevanttia teemaa tee kunnallisvaalien osalta. Eduskuntavaalien osalta toki maahanmuutto on erittäin relevantti teema mutta kunnan- ja kaupunginvaltuustoilla ei ole mitään valtaa Suomen maahanmuuttopolitiikkaan joten noiden vaalien osalta se käytännössä täysin epärelevantti teema.

 

[pekka666]

Näyttää persut vielä tekevän nousua tässä ääntenlaskennan edetessä (kun koko maan tilannetta katsoo), mutta ei tästä taida mitään valtavaa jytkyä tulla. Kuitenkin aika kova nousu edellisiin vaaleihin verrattuna. Eniten ehkä itseäni yllättää vihreiden heikko kannatus, odotin ehkä hieman korkeampaa kannatusta. Tosin ääniä on vielä paljon laskematta, joten katsotaan nyt.

 

[inexcess]

Ei tuo siitä relevanttia teemaa tee kunnallisvaalien osalta. Eduskuntavaalien osalta toki maahanmuutto on erittäin relevantti teema mutta kunnan- ja kaupunginvaltuustoilla ei ole mitään valtaa Suomen maahanmuuttopolitiikkaan joten noiden vaalien osalta se käytännössä täysin epärelevantti teema.

Olen vähän eri mieltä.

Kuntatasolla päätetään vuokra-asuntotuotannosta. Kuntien asuntolautakunnissa myös päätetään kunnan vuokra-asuntojen jakokriteereistä. Toki jakoperusteet täytyy perustua lakiin, eikä ne saa olla syrjiviä, mutta joka tapauksessa kunnalla on päätösvaltaa asiassa.

Pakolaiskeskusten perustaminen päätetään kuntatasolla.

Kuntatasolla myös päätetään, paljonko investoidaan kotouttamispalveluihin, pakolaiskoordinaattoreihin, paperittomille tarjottaviin ilmaisiin palveluihin jne.

 

[JCSH]

Olen vähän eri mieltä.

Kuntatasolla päätetään vuokra-asuntotuotannosta. Kuntien asuntolautakunnissa myös päätetään kunnan vuokra-asuntojen jakokriteereistä. Toki jakoperusteet täytyy perustua lakiin, eikä ne saa olla syrjiviä, mutta joka tapauksessa kunnalla on päätösvaltaa asiassa.

Pakolaiskeskusten perustaminen päätetään kuntatasolla.

Kuntatasolla myös päätetään, paljonko investoidaan kotouttamispalveluihin, pakolaiskoordinaattoreihin, paperittomille tarjottaviin ilmaisiin palveluihin jne.

No sitten kannattaisi puhua niistä vuokra-asunnoista eikä siitä maahanmuutosta mihin sillä kaupunginvaltuustolla ei ole mitään valtaa.
Vastaanottokeskusten perustamisesta päätetään kuntatasolla vain jos sitä ollaan perustamassa kunnan omistamaan kiinteistöön. Jos kyseessä on yksityiseltä vuokrattu tai valtion omistama kiinteistö niin sitten kunnalta ei tarvitse kysyä.

Ja joo, kotouttamispalveluista ja vastaavista päätetään osittain kunnallistasolla. Mutta noissakaan ei ole kyse niinkään maahanmuuttopolitiikasta vaan siitä että mitä tehdään sitten kun ne ovat jo muuttaneet maahan. Ja en ainakaan itse ole nähnyt persuilta hirveän paljon fokusta siihen että miten pitäisi toimia sitten kun maahanmuuttajat ovat maassa vaan he enemmänkin ovat keskittyneet siihen miten pitäisi estää että he eivät ylipäätänsä pääse maahan.

 

[shaminy]

Hallitukselle vahva mandaatti. Ei tullu jytkyä eikä siten hallituskriisiä. Nyt lasketuista äänistä Hallituspuolueet ovat saaneet 57.2%.

 

[Paapaa]

Jokaiselle joka on politiikkaa seurannut viimeiset 10 vuotta, on ollut selviö ettei Perussuomalaisten 18-19% kuntavaalikannatus realisoidu.

Aa, muistelin että Persujen tuloksia aina manipuloidaan todellisuutta pienemmäksi gallupeissa. Mutta se olikin nykyään siis toisinpäin. Tämä selvä!

 

[inexcess]

Aa, muistelin että Persujen tuloksia aina manipuloidaan todellisuutta pienemmäksi gallupeissa. Mutta se olikin nykyään siis toisinpäin. Tämä selvä!

Älä vääristele sanomisiani. Me keskustelemme nyt kuntavaaleista emmekä eduskuntavaaleista.

Eduskuntavaaleissa Persujen kannatus on perinteisesti aina arvostettu alakanttiin. Tämä siitäkin huolimatta, että eduskuntavaaleissa suhteellisen luotettavan gallup-mittauksen tekeminen pitäisi olla selvästi helpompaa.

Kuntavaaleissa painottuu paikallisuus ja paikalliset tekijät. Tämä yhdistettynä 309 kuntaan Suomessa saa aikaan sen, että kuntavaaligallup 2000 haastateltavan otannalla ei voi mitenkään antaa luotettavaa lopputulosta.

Ps. Olen sanonut aina, että gallupeista tulisi julkistaa raakadata, eikä mitään erilaisiin kertoimiin perustuvia manipuloituja lukuja.

 

[Grazer]

Onhan tämä kepulle siinä mielessä torjuntavoitto, että tulosennusteen mukaan kannatusprosentti pysyy juuri ja juuri persujen edellä. Valtuutettuja kepulla toki on edelleen ylivoimaisesti eniten.
Vihreiden mahalasku ihmetyttää. Onko Vihreät saavuttaneet nyt kyllästyspisteensä, kun vihreitä arvoja löytyy olosuhteiden pakosta jo muistakin puolueista?

Fun fact. Entisen kotikaupunkini Salon lopputulos näyttää tällä hetkellä 11 paikkaa jokaiselle Kok, Kesk, PS, SDP. Tuleekohan tappelu valtuuston puheenjohtajan paikasta? Eikä pysty tekemään edes lehmänkauppaa hallituksen puheenjohtajan paikasta kun kaikilla suurilla on sama paikkamäärä. Jämäpaikat Vihreille, Vasemmistoliitolle ja Liike Nytille.
EDIT: Kepulla ollut tuolla vaaliliitto kristillisten ja RKP:n kanssa. Ovat pelastaneet mitä pelastettavissa on.

 

[Paapaa]

Kuntavaaleissa painottuu paikallisuus ja paikalliset tekijät. Tämä yhdistettynä 309 kuntaan Suomessa saa aikaan sen, että kuntavaaligallup 2000 haastateltavan otannalla ei voi mitenkään antaa luotettavaa lopputulosta.

Mutta ei kyse ole vain koko maan gallupeista, vaan myös kuntakohtaisista. Esim. Vantaalla povattiin PS:lle jopa 20%:n kannatusta. Gallup tehtiin siis vain vantaalaisille. Tuosta tuloksesta ollaan jäämässä aika kauas. Koko maan osalta nimenomaan PS:n kannatus näyttää olevan pahasti metsässä. Tässä Ylen tuorein manipulaatio:

Ylen kuntavaalimittaus: Kokoomus jatkaa johdossa, SDP luisuu ja keskustan kannatus osoittaa elpymisen merkkejä

Kokoomus lähtee ennakkosuosikkina kuntavaaleihin. Toisena tulevien perussuomalaisten äänestysvarmuus on kysymysmerkki ja kolmanneksi sijoittuvan pääministeripuolue SDP:n kannatus sulaa kiihtyvällä vauhdilla ennen vaalipäivää.

yle.fi

Erityisesti Kokoomuksen ja PS:n kohdalla ennusteet pielessä - mutta eri suuntiin. Muilla ennusteet huomattavasti paremmin todellisuutta vastaavia. Mutta tämän toki kaikki 10 vuotta politiikkaa seuranneet tiesivät.

Yksi syy on varmaan alhainen äänestysinto. Se sataa usein Kokoomuksen laariin. Kannattaa äänestää.

 

[Grazer]

Yksi syy on varmaan alhainen äänestysinto. Se sataa usein Kokoomuksen laariin. Kannattaa äänestää.

Jep. Ei ole sattumaa että vaaleista toiseen Kauniaisissa on maan korkein äänestysprosentti. Siellä toki RKP on kaikista suurin.

Persuille vaalit on paikkamäärissä katsottuna rökälevoitto. Kepu voi sentään vähän huokaista helpotuksesta, että ihan kaikki persujen lisäpaikat eivät onneksi ole heidän jyvälaaristaan peräisin.

 

[rodder]

Demarit tilasi vaalien siirron ja se toteutui. Änestysprosentti laski eli voittiko demokratia näissä valeissa? Omasta mielestäni Vaalien siirto oli virhe ja se konkretisoituu äänestysaktiivisuudessa.

 

[shaminy]

Päivän paras uutinen. Ei enää sekoilua Oulun valtuustossa!

 

[Paapaa]

Päivän paras uutinen. Ei enää sekoilua Oulun valtuustossa!

Tämäkin ihan hyvä:

Kansanedustaja Ano Turtiainen ei pääse kotikunnassaan Juvalla kunnanvaltuustoon. Hän sai 61 ääntä. Turtiainen pyrki valtuustoon omalta yhden hengen listaltaan.

Lähde: Hs.fi

 

[ATE]

Vähän ehkä yllättävä toi PS:n tulos Helsingissä. Tällä hetkellä +/- 0 paikkaa PS:lle. Tai jotenkin olin kuvitellut, että Halla-aho repisi missä tahansa Jeesus-äänisaaliin. Mutta ei välttämättä pärjää Valtonen-Vartiainen -kaksikolle.

Tähän voi olla syynä että osa persuista on pelannut varman päälle ja äänestänyt kokoomusta ihan sen vuoksi ettei kaupunki saisi vihreää pormestaria.

Tällä hetkellä näyttää kahta lisäpaikkaa Helsingissä persuille.

 

[shaminy]

Tähän voi olla syynä että osa persuista on pelannut varman päälle ja äänestänyt kokoomusta ihan sen vuoksi ettei kaupunki saisi vihreää pormestaria.

Tällä hetkellä näyttää kahta lisäpaikkaa Helsingissä persuille.

Vartiainen on enemmän liberaali ja vihreä kuin Sinnemäki. Vartiaine mm vaatii ehdottomasti ruuhkamaksuja, Sinnemäki ilmoitti että se pitää säilyttää optiona.

 

[JCSH]

Tampereella pormestarin pesti lopulta kiinni 26 äänestä. Muistutus siitä miten kunnallisvaaleissa se yksikin ääni voi oikeasti olla ratkaiseva.