Eramaankettu
Lost and Forgotten
- Liittynyt
- 03.01.2017
- Viestejä
- 2 150
Hola,
Aika moni ymmärtää, että metalleilla lämpö laajentaa. Se on aika selkeää, kun kappale lämpenee tasaisesti. Esimerkiksi laakeri joka on siis pyöreä muoto, niin kasvaa sekä sisämitaltaan, että ulkomitaltaan ja se on näin helpompi saada paikalleen esimerkiksi mitaltaan täysin samanpaksuisen akselin päälle.
Homma muuttuu monimutkaisemmaksi, kun kappale on niin suuri, ettei sitä voi lämmittää kokonaan. Kun sinulla on reikä (200mm) ja kappale on useita metrejä ja mahdollisuuksia ei ole käytännössä tai teoriassa kun lämmittää muutamia kymmeniä senttejä reijän ympäriltä.
Pieneneekö reikä, koska lämpölaajeneminen tapahtuu vain reijän suuntaan, koska siellä on pienin fyysinen vastus?
Reikä pysyy "saman kokoisena ja lämpölaajeneminen tapahtuu vain paksuudessa"
vai yksinkertaisesti reikää ei voi pienentää lämmittämällä vaan reikä aina suurenee lämmittämällä.
Kiitos vastanneille ja jos teillä on jotain fakta linkkejä tms, niin kelpaa myös oivasti.
IMO, reikä pienenee, koska lämpölaajeneminen tapahtuu helpoiten siihen suuntaan - haukkukaa pois.

ee. Kiitokset tosiaan kaikille osallistuneille ja varsinkin @mti:lle hyvin perustellusta vastauksesta sekä kaikille muille keskusteluun osallisuneille ja äänestäneille. Todellisuutta juuri tässä tapauksessa on kait "mahdotonta todistaa näillä resursseilla", mutta halusin tietää onko tämä edes teoriassa mahdollista. Monen laista olen nähnyt ja kokenut pienen ikäni aikana ja fysiikan tuntemus on jossain määrin aina auttanut ymmärtämään mitä edes kannattaa yrittää tehdä. Tässä tapauksessa en voi sanoa kuin, että vaikka yritin aloittaa lämmittämisen kauempaa ja viedä sitä lähemmäksi, jotta koko kappale lämpenisi ns tasaisesti ei tuota reikää saatu suurenemaan, niin että palikka tulisi helposti ulos. Kaikki kolme ulos tullutta saatiin pihalle vasta kuin kappaleen oli annettu jäähtyä. Olisi toden totta varmaan ollut fiksuinta jäähdyttää palikka sen sijaan, että yrittää lämmittää sitä, mutta minkäs teet kun vehkeet on mitä on.
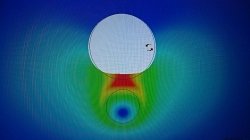
Ollaan tätä kaverin kanssa pari päivää myös pohdittu (kaveri melkein konetekn. DI, minä itse työukko). Tultiin siihen tulokseen, että reikähän se pienenee, kun lämmitetään reiän vierestä yhdestä pisteestä, ja sitä rautaa on reilusti joka suuntaan.
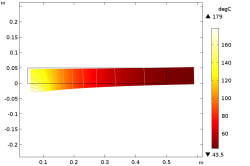
Esimerkinomaisesti kokeiltiin hommaa myös FEMillä, ja tulos suoraan kaverin sanoin: "Metrinen reikä 10 mm levyssä ja lämmittää puolen metrin säteiseltä ympyrältä noin puolen metrin päästä 300 asteiseksi, ni menee lämmitettävältä puolelta max 1 mm kiinni ja leviää hitusen sivuille."
Levyn paksuutta kasvatettaessa ei reiän koon suhteen olennaista muutosta, kiinni menee silti.
Tässäpä kuva (on skaalailtu asian havainnollistamiseksi):
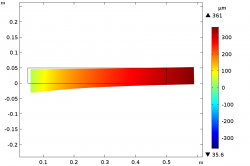
Kuvassa ylempi musta ympyrä tarkoittaa reiän alkuperäistä asemaa, ja väriskaala siirtymää (sininen 0 mm, punainen reilu 1 mm, muut sitten siitä väliltä). Alempi mustaviivainen ympyrä on sitten se lämmitetty alue.
-------
Edit: Sama tapahtunee, vaikka lämmitettäisi kehää y.o. viestin mukaisesti koko reiän ympäriltä, jos ulkopuolella on kylmää materiaalia riittävästi (eikä edes tarvita kovin paljoa). Simuloidaan kun ehditään.
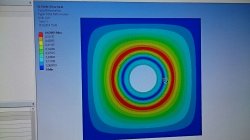
Noniin, nyt on simuloitu taas vähän lisää. Ensimmäisessä kuvassa simuloitiin reiän ympärillä olevan kehän lämmittämistä, ja pidettiin kappaleen ulkoreunat paikoillaan sillä ajatuksella, että todellisuudessa kappale ei ole tuollainen irtonainen, vaan kiinni sieltä täältä "muodonmuutoksia vastustavasti". Lopputuloksena reiän pieneneminen:
Toisessa simulaatiossa kappaleen annettiin laajeta muuten vapaasti, mutta reiän vasemman puoleisin piste kiinnitettiin liikkumattomaksi. Tällöin reikä suureni:
Sen suurempaa päätelmää ei näistä tietty voida vetää tuntematta todellisen kappaleen mittoja, muotoa ja siihen kiinnittyviä muita osia. Toivottavasti näistä nyt jotain suuntaa-antavaa apua kuitenkin on.
Homma muuttuu monimutkaisemmaksi, kun kappale on niin suuri, ettei sitä voi lämmittää kokonaan. Kun sinulla on reikä (200mm) ja kappale on useita metrejä ja mahdollisuuksia ei ole käytännössä tai teoriassa kun lämmittää muutamia kymmeniä senttejä reijän ympäriltä.
Pieneneekö reikä, koska lämpölaajeneminen tapahtuu vain reijän suuntaan, koska siellä on pienin fyysinen vastus?
Reikä pysyy "saman kokoisena ja lämpölaajeneminen tapahtuu vain paksuudessa"
vai yksinkertaisesti reikää ei voi pienentää lämmittämällä vaan reikä aina suurenee lämmittämällä.
Kiitos vastanneille ja jos teillä on jotain fakta linkkejä tms, niin kelpaa myös oivasti.
IMO, reikä pienenee, koska lämpölaajeneminen tapahtuu helpoiten siihen suuntaan - haukkukaa pois.


ee. Kiitokset tosiaan kaikille osallistuneille ja varsinkin @mti:lle hyvin perustellusta vastauksesta sekä kaikille muille keskusteluun osallisuneille ja äänestäneille. Todellisuutta juuri tässä tapauksessa on kait "mahdotonta todistaa näillä resursseilla", mutta halusin tietää onko tämä edes teoriassa mahdollista. Monen laista olen nähnyt ja kokenut pienen ikäni aikana ja fysiikan tuntemus on jossain määrin aina auttanut ymmärtämään mitä edes kannattaa yrittää tehdä. Tässä tapauksessa en voi sanoa kuin, että vaikka yritin aloittaa lämmittämisen kauempaa ja viedä sitä lähemmäksi, jotta koko kappale lämpenisi ns tasaisesti ei tuota reikää saatu suurenemaan, niin että palikka tulisi helposti ulos. Kaikki kolme ulos tullutta saatiin pihalle vasta kuin kappaleen oli annettu jäähtyä. Olisi toden totta varmaan ollut fiksuinta jäähdyttää palikka sen sijaan, että yrittää lämmittää sitä, mutta minkäs teet kun vehkeet on mitä on.
Viimeksi muokattu: